Ich wollte neulich den Stoff der vorhergehenden Stunde wiederholen und sichern, weil der Kurs mir ein wenig damit zu fremdeln schien. Also begann ich mit der Ankündigung, dass wir jetzt etwas gaaaanz anderes machen würden.

Zur Wiederholung

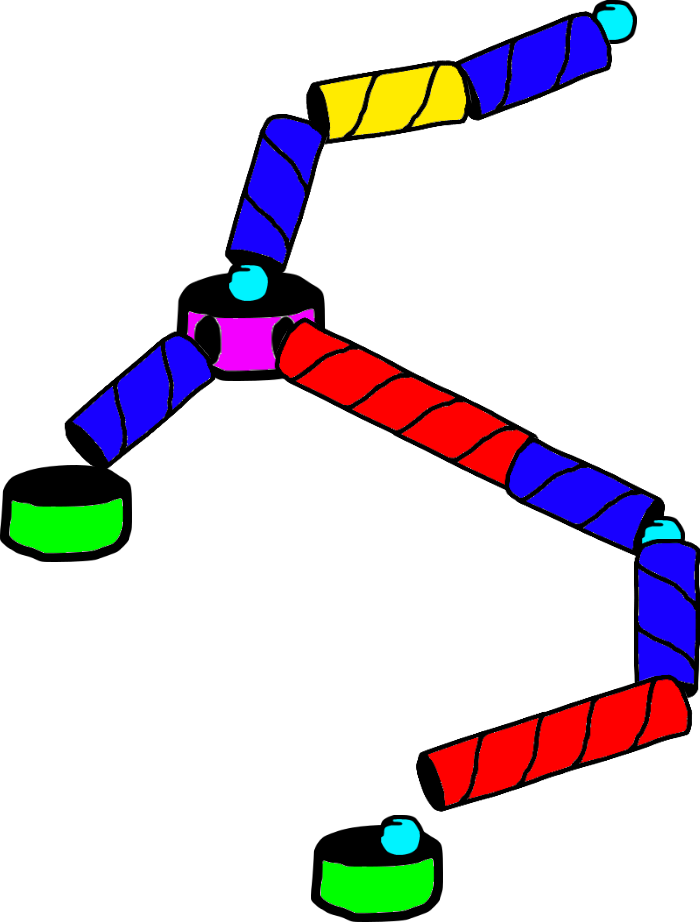
Und zwar hatte ich hier das schöne Foto einer selbstgebastelten Kugelbahn aus Klopapierrollen gefunden. Nicht frei verwendbar, also verlinke ich nur darauf und zeige stattdessen eine Zeichnung von mir, die natürlich schon wieder ein wenig mehr von der Vorlage abstrahiert:

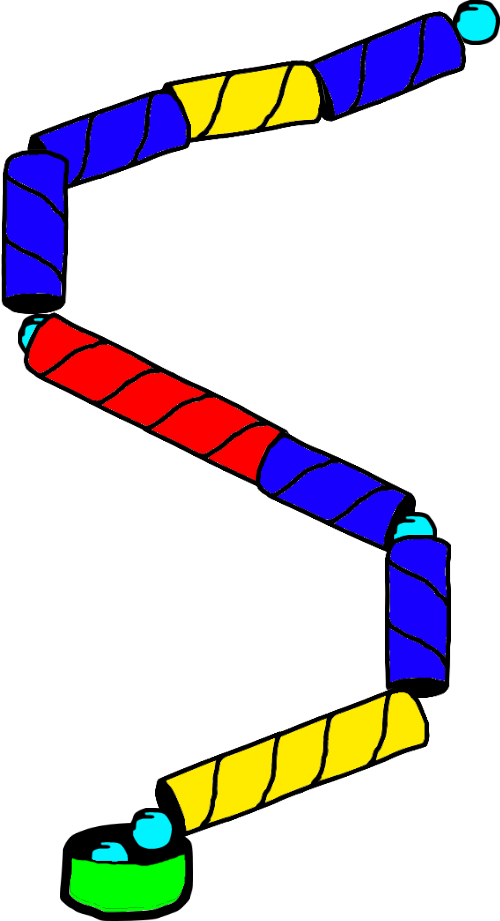
Wir wollen, so die Aufgabe, eine solche Kugelbahn als Programm nachbauen, und das heißt erst einmal: Modellieren, ein Modell entwickeln. Davor wiederum müssen wir entscheiden, wozu wir das Modell brauchen. Geht es darum, herauszufinden, wie sich das Material der Kugel auf das Verhalten beim Spielen auswirkt – Metall, Holz, Tischtennisball? Oder das Material der Klopapierrollen – Holz, Plastik, Metall? Oder wollen wir den Einfluss der Schwerkraft untersuchen, also wie sich eine Kugelbahn auf dem Mond verhalten würde? Nein, wir wollen, so die Vorgabe, nur eine Kugelbahn für ein einfaches Spiel haben, bei dem man sich Bahnen zusammenklicken kann und womit man Fünfjährige unterhalten kann. Das heißt, wir brauchen keine physics engine, keine Simulation von Schwerkraft und Reibung und so weiter.

Ein erster Schritt beim Modellieren: Was brauchen wir für Objekte? Im Bild oben zähle ich vierzehn Objekte. Die Frage nach den Eigenschaften der Objekte könnte man hier schon stellen, aber ich mache das gleich zusammen mit dem nächsten Schritt.

Dann nämlich: Kann Ähneln sich die Objekte so, dass eine Aggregation möglich ist, dass ich also Klassen dazu anlegen kann? Im Fall oben wären das sicher die Klassen: Kugel, Röhre, Auffangbehälter. Die Kugel hätte – vielleicht – das Attribut Geschwindigkeit, zum Auffangbehälter fallen mir erst einmal keine Attribute ein, bei den Röhren gibt es: Farbe, Länge, und Neigungswinkel. Als Klassendiagramm sieht das so aus:

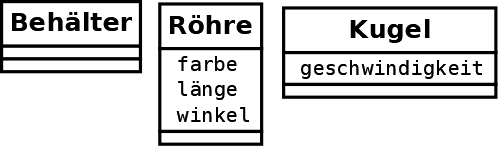
Der nächste Schritt: Welche Beziehungen gibt es zwischen den Elementen? Das heißt manchmal auch Strukturanalyse. Da kommt dann zum Beispiel heraus, dass jede Röhre eine Nachfolgerröhre hinten dran hat, an die sie die Kugel weiterreicht. Allerdings stimmt das nicht ganz: eine Röhre hat entweder eine weitere Röhre hinten dran oder einen Auffangbehälter. So ein Oder lässt sich mit einer gemeinsamen Oberklasse lösen, die ich hier Röhrenelement nenne:

Jeder Behälter ist auch ein Röhrenelement, und jede Röhre ist ein Röhrenelement; das bedeuten die Pfeile mit den Dreiecksspitzen. Und jede Röhre hat 1 Röhrenelement als Nachfolger. Das kann dann eine weitere Röhre sein, oder ein Behälter.

(Es gibt hier keine unmittelbare Beziehung zwischen Kugel und Röhre, darüber kann man streiten, wie man überhaupt über alles beim Modellieren streiten können sollte. Das ist hier aber nicht wichtig. Und es ginge zur Not auch anders, man könnte Röhre und Behälter zusammenmischen; eine Röhre könnte dann eben auch keinen Nachfolger haben, und wäre dann ein ARt improvisierter Behälter.)

Außerdem hat jedes Röhrenelement eine Methode empfangeKugel. Diese Methode sieht in den Unterklassen aber jeweils unterschiedlich aus, der Behälter macht einfach nichts mit der Kugel, wenn er sie empfängt, ein Röhrenobjekt macht schon etwas, nämlich es gibt sie an die nächste Röhre weiter. (Dazwischen kann es die Geschwindigkeit der Kugel verändert haben, je nach Länge und Neigungswinkel. Auch die Dauer zum Durchlaufen könnte hier angepasst werden, die habe ich aber noch gar nicht modelliert.)

Und wir haben, wie geneigte Oberstufenschüler und -schülerinnen schon erkannt haben, das Kompositum-Muster.

Exkurs: Das Kompositum

Das Kompositum-Entwurfsmuster taucht in der Informatik immer wieder mal auf, und zwar vor allem bei Elementen von grafischen Benutzeroberflächen. Es ist praktisch, wenn es darum geht, etwas zu gruppieren. Elementen. In der (jetzt) 12. Jahrgangsstufe Informatik ist das Kompositum-Entwurfsmuster Pflicht, und zwar im Zusammenhang mit den einfach verketteten Listen. Ich bin nicht ganz glücklich darüber, weil diese unsere Listen ohnehin bereits künstlich umständlich gehalten sind (nämlich ohne Referenz auf das Ende, und ohne Längenattribut, so dass halt jedesmal neu durchgezählt wird) und weil das Kompositum-Muster mir hier ein nicht ganz typischer Fall zu sein scheint. Aber muss halt, und sieht dann am Ende so aus:

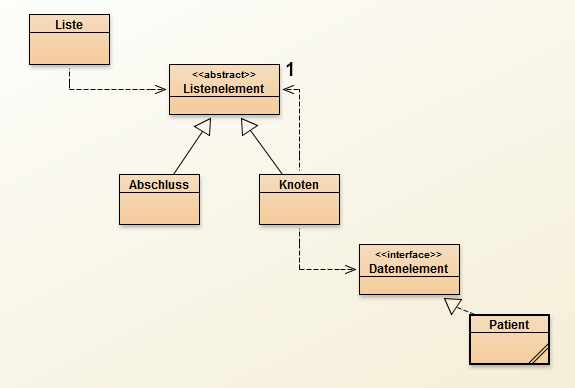
Der Kerngedanke: Es gibt Elemente, die einen oder meist mehrere Nachfolger haben (die heißen: Kompositum), und andere Elemente, die keinen Nachfolger haben (die heißen: Blatt). Zusammengehalten wird beides durch eine abstrakte, also nie unmittelbar verwendete, Oberklasse (heißt: Komponente), und kein Objekt weiß von seinem Nachfolger, ob der jetzt ein Blatt ist oder ein Kompositum, sondern kennt es nur als Komponente. Mehr steht bei Wikipedia.

Vorteile des Kompositum-Musters

Wenn man das Modell erweitern möchte, etwa um Röhren, die halb durchsichtig sind, oder Röhren, die eine kleine Glocke eingebaut haben, so dass die Kugel beim Durchgehen bimmelt (kann man auf dieser Bastelseite sehen, auch als Video, ebenfalls ein Klorollenmodell), dann geht das leicht. Man muss sich nur überlegen, ob man dafür ein zusätzliches Attribut (mit Glocke oder ohne) anlegen möchte, oder eine zusätzliche Röhren-Unterklasse (für Durchsichtigkeit). Das ist eine Designfrage, im Diagramm habe ich mal das eine, mal das andere verwendet:

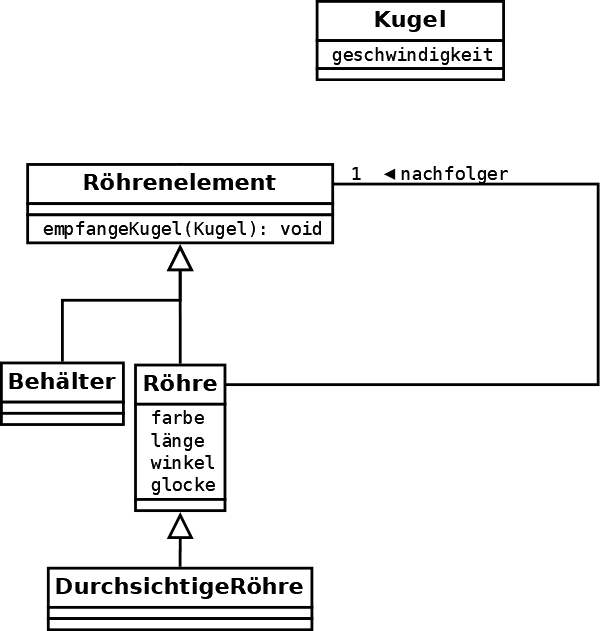
Der eigentliche Vorteil ist aber der, wenn ich ganz neue Elemente haben möchte. Das kommt bei den Listen in der Schule überhaupt nicht vor, weil es da nur ein Kompositum-Element gibt. Für die Kugelbahn schlage ich ein zweites vor, den Verteiler, der die hereinkommende Kugel zufällig an einen von zwei möglichen Ausgängen weiterleitet:

Dafür lohnt sich sicher eine eigene Klasse, zumal sich hier etwas Grundsätzliches ändert – ein Verteiler hat zwei Nachfolge-Elemente:

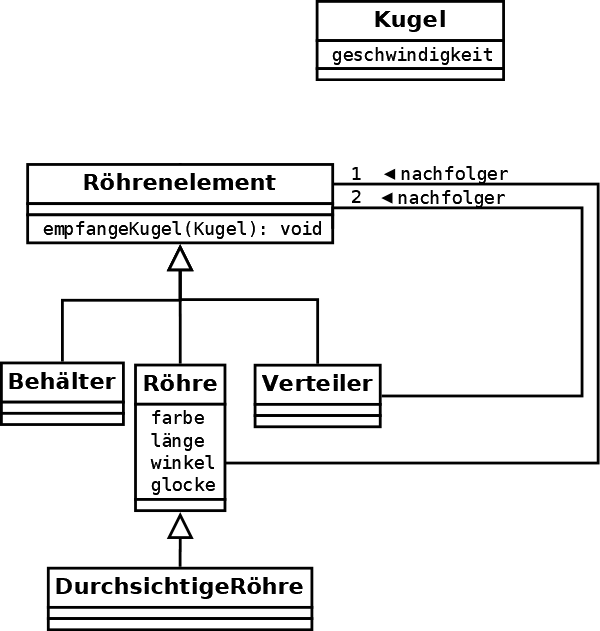
Das lässt sich bequem ins Kompositum-Muster einbauen, ohne dass man an den anderen Klassen etwas verändern muss. Ebenso kann man sich nach und nach leicht weitere Bausteine einfallen lassen, ohne dass man an den bestehenden Klassen etwas ändern muss, was nicht ginge, wenn man ohne Kompositum arbeiten würde. Da wäre der Looping, und der Dreierverteiler, die Teleportröhre…

(Was ist, wenn man eine Art Sackgasse mit Sprungfeder möchte, so dass eine Kugel wieder in das vorherige Element zurückspringt, eine Art Trampolin? Da gibt es mehrere Möglichkeiten. Entweder jedes Element hat nicht nur einen Nachfolger, sondern auch einen Vorgänger, wie die doppelt verkettete Liste, oder man macht das so wie in Buch und Lehrplan, nämlich recht umständlich.)