(Aus der Reihe: Alles muss raus. Angefangene Blogbeiträge des Jahrs 2008 aufräumen. Diesmal wohl nur für Mathematikfreunde.)
Vieles zum Braess-Paradoxon steht in Wikipedia. Auch die Illustrationen in diesem Blogbeitrag habe ich daraus genommen (Autor AlterVista, CC-BY-SA 3.0, Details hinter dem Link). Eigentlich wollte ich das selber und anders zeichnen, aber ich komme wohl doch nicht dazu.
Der Kern des scheinbaren Paradoxons ist der, dass eine Situation verschlechtert werden kann, wenn man eine weitere, optionale Alternative anbietet. Man baut zum Beispiel eine neue, zusätzliche Straße, und es gibt mehr Staus. Oder auch umgekehrt: man sperrt eine vorhandene Straße, und plötzlich kommen alle schneller voran.
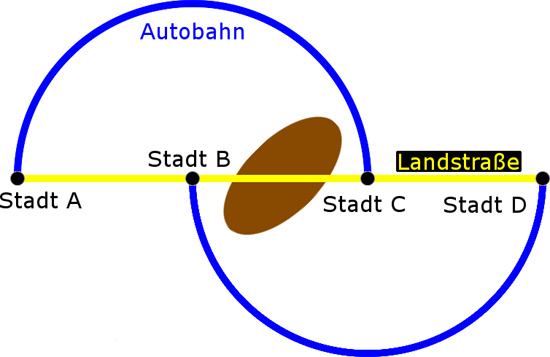
Man stelle sich wie in dieser Zeichnung die vier Orte A, B, C und D vor. Verbunden sind sie auf folgende Weise durch Autobahnen (blau) beziehungsweise Landstraßen (gelb):

Die Landstraßen sind relativ kurz, verstopfen aber auch schneller bei viel Verkehr. Man braucht für die gelben Strecken also 10 mal x Minuten, wobei x die Anzahl der Autos auf der Strecke ist (in Tausendern, der Einfachkeit halber). Sind 2000 Autos unterwegs, braucht man 10 mal 2 Minuten, bei 4000 Autos sind es schon 40 Minuten.
Die blauen Strecken sind länger, aber besser ausgebaut und verstopfen nicht so schnell Man braucht für sie 50 plus x Minuten, wobei x wieder die Zahl der Autos auf der Strecke ist (in Tausendern). Bei 2000 Autos braucht man 52 Minuten, bei 4000 auch nur 54 Minuten.
Wenn Autofahrer von A nach D wollen, dann können sie die Route ACD nehmen oder ABD. Nehmen wir an, in einer Stunde wollen 6000 Autos von A nach D. Die Hälfte wird die eine Strecke nehmen, die andere Hälfte die andere. Der Wert von x ist also jeweils 3 (für 3000 Autos):
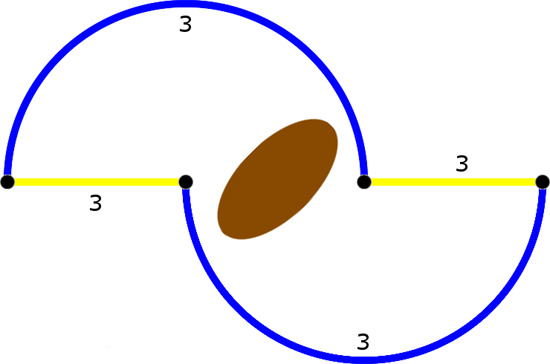
Fahrzeit für jedes Auto: (10 mal 3) + (50 plus 3), also 83 Minuten.
Jetzt wird eine zusätzliche Straße gebaut, ein Tunnel. Fahrzeit: 10 plus x Minuten. Man braucht nicht viel Zeit dafür, auch bei großer Verkehrsdichte.
Auch hier wird sich bald ein Gleichgewicht einpendeln. Unsere 6000 Fahrer von vorhin werden sich wieder so auf die Strecken verteilen, dass jeder gleich viel Zeit benötigt. Dabei werden jeweils 2000 Fahrer die Strecke ABD fahren, 2000 die Strecke ACD und die letzte 2000 Fahrer ABCD. Pro Stunde fahren 4000 Autos auf den Landstraßen und 2000 Fahrzeugen pro Stunde auf den Autobahnen und im neuen Tunnel:
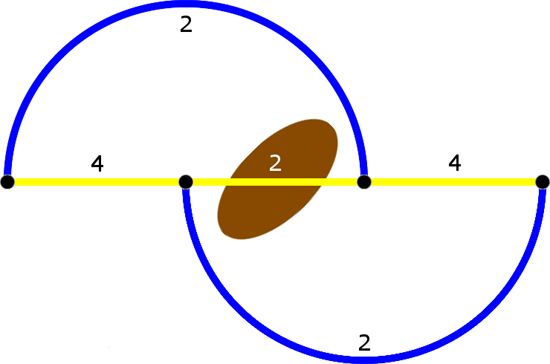
Die Fahrdauer ist jetzt für alle 92 Minuten – neun Minuten länger als ohne die zusätzliche Strecke. Und wenn ein einzelner denkt, er fährt dann halt doch eine der anderen Strecken, dann wird er dort etwas länger brauchen als 92 Minuten (und die Fahrer auf seiner alten Strecke etwas weniger). Wenn alle Fahrer darauf verzichten würden, die neue Strecke zu benutzen, dann wären wieder alle bei 83 Minuten. Aber einer käme vielleicht doch in Versuchung, den Tunnel zu benutzen, und bräuchte nur 70 Minuten. Aber die anderen würden es ihm, so ist der Mensch, gleichtun, und wieder würde sich das Gleichgewicht bei 92 Minuten einpendeln.
(Parallelen zum Gefangenendilemma sind erkennbar.)
Für die Anwendbarkeit im echten Leben siehe Wikipedia. Interessant ist auch der Link dort zum Eisverkäufer-am-Strand-Problem.
Schreibe einen Kommentar