Ein Graph ist wie die verkettete Liste eine dynamische Datenstruktur. Das ist Stoff im Fach Informatik, 11. Klasse, Bayern.
Ein Graph ist im eigentlich nur ein Haufen von Punkten, von denen manche miteinander verbunden sind. Die Punkte heißen auch Knoten und die Verbindungen Kanten. Ein Graph besteht also aus einer Reihe von Knoten und einer Reihe von Kanten; jede Kante verbindet zwei Knoten, und von jedem Knoten geht eine Anzahl von Kanten weg.
So einen Graph kritzelt man ganz schnell auf ein Blatt Papier. „Das ist das Haus vom Nikolaus“ ist ein Graph. Die kleine Karte, die man sich bei einem Computerspiel anfertigt, ist ein Graph (jedenfalls bei den Spielen, die ich so spiele).
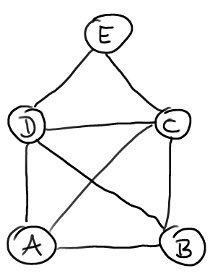
Mit einem Graph kann man das U- und S-Bahn-Netz München modellieren, die Verteilung von Elementen auf einer Leiterplatte, das Königsberger Brückenproblem oder das Straßennetz Deutschlands.
Wenn man dann so eine Situation als Graph modelliert hat und diesen Graphen vielleicht noch auf die eine oder andere Art in einem Computerprogramm umgesetzt hat, dann will man auch etwas mit ihm anfangen. Den kürzesten Weg von einem Knoten zum anderen finden, oder die kürzeste Rundreise, bei der man bei jedem Knoten mindestens einmal vorbeigeschaut hat. Für diese und ähnliche Probleme gibt es mehr oder weniger gute Algorithmen, also genaue – und damit leicht in ein Programm umsetzbare – Lösungsregeln.
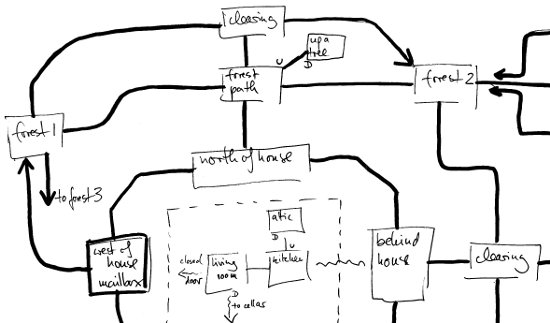
Ein einfaches solches Problem besteht darin, von einem Startknoten aus alle anderen erreichbaren Knoten zu besuchen und dabei keinen zu übersehen. Ein einfacher Algorithmus dazu heißt „Tiefensuche“, und der steht explizit im Lehrplan. Die Tiefensuche erkläre ich hier nicht; ich will nur die Aufzeichnung einer Präsentation dazu zeigen, die ich mal angefertigt aber nie benutzt habe. Die Idee für die Höhlenerkundung als Beispiel der Tiefensuche habe ich aus dem Buch
Informatik. Rekursive Datenstrukturen, Softwaretechnik. Schülerbuch 11. Klasse von Peter Hubwieser, Patrick Löffler und Petra Schwaiger (bei Klett).
(Herunterladen als – etwas schlampig geschriebene – Open-Officen-Datei.)
Andere Algorithmen zum Durchlauf eines Graphen sind etwa die Breitensuche oder der Dijkstra-Algorithmus. Auch den will ich hier nicht groß erklären, obwohl er ziemlich wichtig ist.Ich habe ihn zuerst nicht verstanden, obwohl ich die Erklärung im Buch gelesen habe. Daraufhin habe ich den Algorithmus nach und nach umgeformt, auf Papier gekritzelt, zusammengefasst, und neu für mich formuliert. Dann hatte ich ihn verstanden. Und als ich meine Formulierung mit der im Buch verglich, sah ich, dass da ziemlich genau das gleiche stand.
Mit dem Dijkstra-Algorithmus lassen sich effizient nicht nur irgendwelche Wege im Graphen finden (wie bei der Tiefensuche), sondern jeweils die kürzesten Wege von einem Startpunkt aus zu allen anderen Punkten. Auch dazu gibt es eine Präsentation. Das muss wohl so sein, davon gibt es bei Youtube schon so viele, aber jeder Informatiklehrer muss irgendwann mal seine eigene machen:
(Herunterladen als Open-Office-Datei, dazu noch ein Arbeitsblatt zum Ausdrucken, um das mit dem Bleistift nachzuvollziehen. Nur so kapiert man es.)
Schreibe einen Kommentar