Zum vorhergehenden Beitrag. Der ist inzwischen so lange her, dass ich etwas den Faden verloren habe. Es ging um die Punkte, Noten und Normalverteilung. Jetzt eher wirr, Sie mögen verzeihen, der Rest.
Meine Erkenntnisse bisher: Gesamtpunktzahlen sind tatsächlich mehr oder weniger normalverteilt, zum Beispiel so:
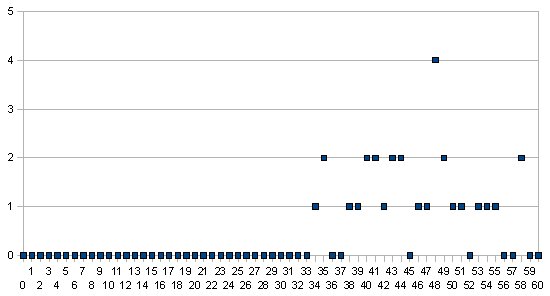
Die abstrakterer Normalverteilungskurve dazu sieht so aus:
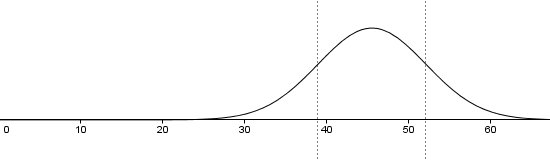
Diese halbwegs normalverteilten Punktezahlen werden dann nach einem äquidistanten Schlüssel in Noten von 1 bis 6 umgerechnet. Das sieht dann so aus:
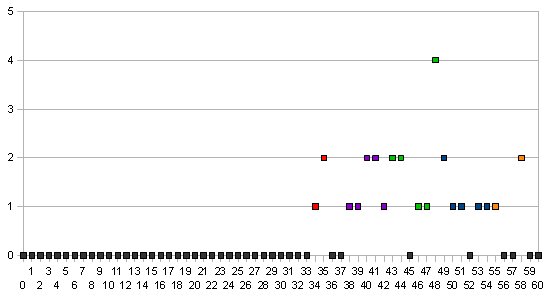
Auch hier wieder die Normalverteilungskurve, wobei die 6 Farben den 6 Noten entsprechen.
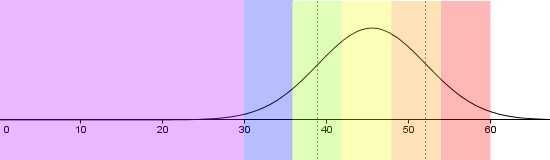
Diese Farbverteilung gilt für eine normal schwere Englischschulaufgabe. (Wären die Aufgaben besonders schwer oder leicht, wäre eine andere Punkteskala angebracht. Dann wären die rechten 5 Farbstreifen jeweils alle etwas schmäler oder breiter.) Die eingezeichnete Kurve ist die einer gut ausgefallenen Schulaufgabe, in der es keine 6 gab und der Mittelwert bei knapp über 3 lag. Die auf der Basis des äquidistanten Punkteschritts entstandene Notenverteilung ist immer noch halbwegs normalverteilt: weniger 1er und 5er, mehr 2er und 4er, noch mehr 3er. Dass es keine 6er gibt, ändert nichts an der Normalverteilung, sondern schiebt die eingezeichnete Kurve einfach etwas nach rechts; bei einem schlechteren Ergebnis muss man sich die Kurve einfach weiter links und eventuell etwas flacher vorstellen.
Genauso gut könnte man allerdings auch einen anderen, nicht äquidistanten Punkteschlüssel verwenden, bei dem die Bereiche für die 1 und 6 viel, die für 2 und 3 ein bisschen größer und die für 3 und 4 kleiner sind. So etwa:

Wenn man den Bereich für die 3 und 4 entsprechend klein, den für 1 und 6 entsprechend groß macht, kann trotz normalverteilten Punktezahlen jede Note etwa gleich oft heraus kommen. (In der Oberstufe wird im Fach Englisch ein solcher nicht äquidistanter Schlüssel angewendet. Der spreizt die Bereiche allerdings nur ein bisschen; die letztliche Notenverteilung ist dann doch wieder normalverteilt. Also steckt da schon der bewusste Wunsch dahinter, zu einer Normalberteilung der Noten zu kommen.)
Ist diese letztlich ja doch angestrebte Normalverteilung an Noten 1-6 als Ziel sinnvoll? Warum nicht mal eine bimodale Verteilung:
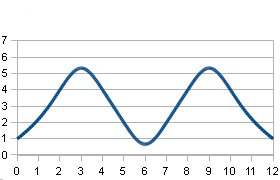
Macht es überhaupt Sinn, sich den Durchschnitt und die Verteilung von Noten anzusehen? Theoretisch ist es so, dass es zwischen den Noten 4 und 5 eine wichtige Grenze gibt: Die Noten 1-4 sind sehr gut bis ausreichend und gelten als „bestanden“. Ausreichend halt. Die Noten 5-6 sind ungenügend oder schlimmer. Eben nicht ausreichend, um zu bestehen. Bei der Benotung von Deutschaufsätzen wird das auch so gehandhabt, bei allen punktezählenden Klausurvarianten wird die Grenze relativ willkürlich auf eine bestimmte Punktzahl festgelegt. Bei diesen wünsche ich mir eine bessere Möglichkeit, ausreichend von nicht ausreichend zu unterscheiden.
Andere Länder
In der Schweiz sieht es übrigens so aus: es gibt Noten von 6 bis 1, dabei ist 6 die beste Note und 1 die schlechteste. Vor allem ist aber die Aufteilung der Noten eine andere: 1-3 ist ausreichend (sehr gut, gut, genügend), 4-6 ist nicht aureichend (ungenügend, schlecht, sehr schlecht). Das wünsche ich mir manchmal auch: weniger Differenzierung bei den ausreichenden Leistungen und mehr bei den nicht ausreichenden.
Auch in Italien ist das wohl so: Da gibt es die Noten 0 bis 10, wobei 10 am besten ist. Die Noten 0-5 entsprechen verschiedenen Graden von nicht ausreichend, die Noten 6-10 sind ausreichend (genügend bis ausgezeichnet).
Ganz extrem finde ich das bei den 15 Punkten der bayerischen Oberstufe: es gibt elf bis zwölf Noten für ausreichend (15 bis 5 oder 4 Punkte, je nachdem wie man es sieht) und gerade mal vier bis fünf Noten für nicht ausreichende Leistungen (4 oder 3 bis 0). In welchem Bereich ist eine möglichst differenzierte Rückmeldung denn sinnvoller? Das weiß ich noch nicht.
Natürlich liegt die größere Differenzierung im oberen Breich auch daran, dass mehr Schüler Ergebnisse in diesem Bereich erzielen, was ja schön ist. Und an der inflationären Natur von Noten. Wenn alle immer bessere Noten kriegen, muss man halt oben anbauen. So führt England 2009/10 auch bei den A-Levels die Note A* ein, weil es einfach zu oft A gibt.
(Mehr zu Noten in verschiedenen Ländern bei Wikipedia.)
Leistungen und das Leben danach
Vermutlich unterscheiden sich die Noten in den verschiedenen Bundesländern nicht sehr von einander. Allerdings scheint es so zu sein, dass aus vielerlei Gründen die Schüler in einem Bundesland, sagen wir mal, bessere Leistungen erzielen als in, sagen wir, einem anderen Bundesland. Das können internationale oder bundeslandübergreifende Tests ergeben. Darauf ist dann das eine Bundesland stolz.
Meine Vermutung ist: zu Recht. Aber sicher bin ich mir nicht. Wer mehr in der Schule lernt und wer mehr nach der Schule kann, muss nicht unbedingt ein glücklicheres oder produktiveres Leben führen, auch wenn ich das vermute. Das zu untersuchen ist wichtiger, aber auch schwieriger.
Ich erinnere nur an diese Studie, deren Ergebnisse nahelegen, dass über das Leben nach der Schule nicht das Schulsystem entscheidet (Gesamtschule, Dreigliedrigkeit), sondern immer noch die soziale Herkunft der Familie: „Wenn es um die weiteren Bildungsstufen geht, um die risikobehafteten Entscheidungen beim Schulabschluss, bei der Ausbildung und bei den Berufslaufbahnen, dann verliert sich dieser schulische Einfluss, und die familiären Ressourcen in der Gestaltung der Entscheidungen treten in den Vordergrund.“
Die Vergleichsarbeiten
Bei den Vergleichsarbeiten in der 8. Jahrgangsstufe gibt es für jede Aufgabe nur einen Punkt: Gelöst oder nicht gelöst. Der Schwierigkeitsgrad der verschiedenen Aufgaben ist den Testauswertern bekannt, und abhängig davon, wie viele Aufgaben welchen Schwierigkeitsgrads gelöst worden sind, lässt sich – theoretisch – errechnen, auf welchem Leistungsstand der Schüler ist.
(Deshalb macht es bei diesen Aufgaben auch wenig Sinn, die Punkte zu summieren, also den Prozentsatz an gelösten Aufgaben zu errechnen. Es kommt darauf an, welche Aufgaben gelöst wurden. Zugegeben, wenn man wollte, könnte man das schon hochrechnen, jedenfalls wenn man den Schwierigkeitsgrade der Aufgaben kennte.)
Punkte bei Teilaufgaben
Zufrieden war ich neulich bei einer Prüfung, die ich gestellt habe. Stoff der letzten Stunde, plus etwas Grundwissen. Es gab eine Aufgabe, die das mir Wichtigste enthielt: wer die nicht schaffte, bei dem sah ich die Leistung insgesamt als nicht ausreichend. Note 5 oder 6. Dazu gab es zwei kleinere Aufgaben, die darüber entschieden, in welchem Abschnitt von „ausreichend“ sich die Leistung bewegen würde (falls die erste Aufgabe gelöst war), die machten also den Unterschied zwischen 1-4 aus.
Schreibe einen Kommentar