Beim letzten Mal ging es um die technische Seite der Normalverteilung. Diesmal erzähle ich, wie es überhaupt dazu kam, dass ich mir darüber Gedanken machte. Das war so:
Einmal schrieben alle Klassen eines Jahrgangs an unserer Schule die gleiche von uns Lehrern selbst entworfene Prüfung. Sie bestand aus 13 Teilaufgaben; auf jede Aufgabe gab es 3-6 Punkte. Insgesamt waren 60 Punkte zu erreichen. Von drei Klassen hatte ich die Ergebnisse in digitaler Form zur Verfügung, das waren 87 Schüler (ohne Legastheniker und Sonderfälle). Wo ich schon mal so viele Ergebnisse hatte, bot es sich an, die auch mal genauer anzuschauen.
Ein erster Überblick über die Gesamtpunktzahlen, auf der x-Achse die Punkte von 0 bis 60, auf der y-Achse die Summen der erreichten Punkte, schon ein bisschen geglättet:
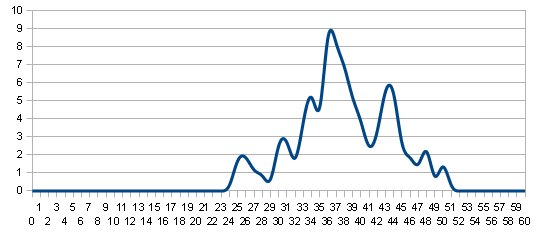
Unspektakulär. Normalverteilt genug, auch wenn da ein Loch rechts neben der Mitte ist.
Mich hat jetzt besonders interessiert, welche der einzelnen Teilaufgaben uns Prüfungserstellern gut gelungen sind und welche nicht. Ich verrate bestimmt kein großes Geheimnis, wenn ich zugebe, dass man manchmal mit Aufgaben daneben langt. Sie sind zu leicht oder zu schwer oder falsch oder ungeeignet dazu, das zu prüfen, was man damit prüfen will. Ich dachte mir beim Betrachten unserer Prüfungsergebnisse erst mal ganz naiv: Eine Aufgabe mit, sagen wir, 5 Punkten, bei der jeder Schüler nur 0-2 Punkte erreicht hat, war möglicherweise zu schwer. Eine Aufgabe mit 5 Punkte, bei der jeder Schüler 4-5 Punkte erreicht hat, war vielleicht zu leicht und differenziert nicht besonders. Gerade beim Benoten solcher Aufgaben läuft es manchmal darauf hinaus, dass man die Aufgaben, bei denen alle Schüler gleich gut oder gleich schlecht waren, genauso gut gleich hätte weglassen können, so dass die tatsächliche Note eigentlich nur von den wenigen differenzierenden Aufgaben abhängt.
Ich ließ also mein Auge die Spalten des Tabellenkalkulationsprogramms hinabgleiten. In jeder Spalte standen die Ergebnisse einer Aufgabe. Gab es ständig nur hohe Zahlen… zu leicht… gab es ständig nur kleine Zahlen… zu schwer… und weil ich gerne bastle, hoffte ich darauf, dass es vielleicht eine schicke Funktion geben würde, die mir das Rechnen abnimmt und mir auf Basis der eingegeben Zahlen einfach ausgerechnet, wie gut oder schlecht die einzelnen Punkte verteilt waren.
Ah! Daher die Beschäftigung mit der Standardabweichung. Leider hat sich – siehe letzten Eintrag – herausgestellt, dass mir die vermutlich nicht viel weiterhilft. Zumindest ist mir hier noch weniger klar, wie man da von einer Summe unabhängiger Einzeleregebnisse sprechen soll. Außerdem gibt es ja auch noch eine Mittelabweichung, und ich als völliger Laie habe keine Ahnung, ob die nicht ohnehin angebrachter ist. Oder ob das ganze überhaupt Käse ist. Aber völlige Laien schreckt so etwas nicht ab, also habe ich mir eine Tabelle gebastelt und damit experimentiert:
- Die Standardabweichung allein sagt noch nicht viel aus. Eine Standardabweichung von 1,4 Punkten bedeutet bei einem Mittelwert von 2,5 Punkten etwas ganz anderes als die gleiche Abweichung bei einem Mittelwert von 5,5 Punkten.
- Das kann man ausgleichen, indem man mit dem Quotient aus Standardabweichung und Mittelwert oder maximal erreichbaren Punkten arbeitet. Ist das erlaubt? Holt mich gleich die Statistikpolizei?
- Wenn die Standardabweichung 0 ist, haben alle Schüler das gleiche Ergebnis. Wenn die Standardabweichung etwa gleich dem Mittelwert ist, dann gibt es eigentlich nur Extremwerte – entweder viel oder wenig Punkte und kaum etwas dazwischen.
- Über den Lösungsgrad einer Aufgabe sagt weder die Standardabweichung noch der Mittelwert etwas. Wenn 8 Punkte zu erreichen wären und sich die Leistungen aller Schüler schön auf die Punkte 0-4 verteilen, dann ist die Aufgabe schön differenzierend, aber trotzdem stimmt etwas nicht mit ihr.
- Schön verteilt – dazu weiter unten mehr – sind Ergebnisse dann, wenn der Quotient aus Standardabweichung und Mittelwert um die 0,5 beträgt. Oder der Quotient aus Standardabweichung und maximaler Punktezahl zwischen 0,25 und 0,35. Das sage ich jetzt einfach mal so. Das ist doch schon mal ein Ergebnis, mit dem ich meine Prüfungsaufgaben anschauen kann.
An der Stelle habe ich dann das Handtuch geworfen. Ich gebe auf. Passe. Hier sind die leicht veränderten Werte zu den einzelnen Aufgaben: wem eine schöne Formel einfällt, wie man aus Mittelwert, maximaler Punktzahl, Standardabweichung oder anderem Krimskram ablesen kann, ob einem die Aufgabe gelungen ist, der kann sie ja mitteilen. Vermutlich lernt man im 1. Semester Statistik schon, wie das geht, oder dass das ja mal überhaupt gar nicht geht.
| Aufgabe: | Max. | Mittelw. | Lösungsgr. | Stabw | Stabw/ Mittelw. | Stabw/ Max | Kommentar |
| A | 3 | 2,55 | 85% | 0,71 | 0,28 | 0,24 | zu leicht |
| B | 4 | 3,38 | 84% | 0,86 | 0,26 | 0,22 | sehr hoher Lösungsgrad, wenig Ausreißer |
| C | 4 | 3,31 | 83% | 0,85 | 0,26 | 0,21 | sehr hoher Lösungsgrad, wenig Ausreißer |
| D | 5 | 3,92 | 78% | 1,04 | 0,27 | 0,21 | |
| E | 5 | 3,35 | 67% | 1,30 | 0,39 | 0,26 | differenziert gut |
| F | 6 | 4,01 | 67% | 1,10 | 0,28 | 0,18 | |
| G | 6 | 3,98 | 66% | 1,33 | 0,33 | 0,22 | |
| H | 6 | 3,81 | 63% | 1,35 | 0,35 | 0,22 | |
| I | 5 | 3,05 | 61% | 1,11 | 0,37 | 0,22 | |
| J | 4 | 2,32 | 58% | 0,98 | 0,42 | 0,24 | differenziert gut |
| K | 4 | 1,47 | 37% | 0,91 | 0,62 | 0,23 | geringer Lösungsgrad, differenziert schlecht |
| L | 4 | 1,39 | 35% | 1,07 | 0,77 | 0,27 | geringer Lösungsgrad, differenziert schlecht |
| M | 4 | 1,16 | 29% | 0,97 | 0,84 | 0,24 | differenziert kaum, sehr ähnliche (schlechte) Werte |
Ich habe aber auch deshalb aufgegeben, weil ich auf die darunter liegende unter viel wichtigere Frage gestoßen bin. Wann ist denn eine Verteilung von Punkten schön oder gelungen? Was will ich denn eigentlich erreichen mit einer Aufgabe?
Ah.
Oh.
Was will ich bei einer Aufgabe, für die ich 8 Punkte gebe: will ich, dass alle Schüler 7-8 Punkte kriegen, will ich eine Verteilung über das Spektrum 5-8 oder eine über 0-8? Oder will ich, dass es entweder 0 oder 8 Punkte gibt und nichts dazwischen? Warum? Es hilft natürlich nichts, zu sagen, dass es nicht darauf ankommt, was man als Lehrer will, sondern darauf, was die Schüler leisten. Denn natürlich hängt das Ergebnis dann doch von der Aufgabenstellung ab, ob man sich bewusst für eine entschieden hat oder nicht.
Eigentlich wollte ich meine Überlegungen hierzu auch noch in diesen Blogeintrag packen. Aber die sind dann so unpräzise und durcheinander geworden, dass ich ihnen lieber durch den in Bälde folgenden eigenen Eintrag zumindest den Anschein inneren Zusammenhangs geben möchte. (Vielleicht fällt ja jemand darauf herein.)
Schreibe einen Kommentar