Executive summary: Der Schwierigkeitsgrad mancher Aufgaben bleibt bei wachsender Problemgröße konstant, bei anderen steigt er linear, polynomiell (z.B. quadratisch) oder exponentiell an.
Die Informatik beschäftigt sich unter anderem damit, welche Aufgaben schwierig sind und welche leicht. Es gibt nämlich schwierige und leichte Aufgaben. Eine Deutschstunde vorzubereiten, das ist leicht; eine Deutschklausur zu korrigieren, das ist schwer. Oder war das doch umgekehrt? Wie misst man die Schwere von Aufgaben?
Bei einem gängigen Ansatz in der Informatik (es gibt noch andere) interessiert man sich dafür, wie lange man für eine Aufgabe braucht. Das heißt dann Zeitkomplexität.
Allerdings misst man diese Länge nicht in Sekunden oder Minuten oder Jahren, denn wie schnell eine Lösung gefunden wird, hängt ja auch vom individuellen Arbeitstempo eines Menschen oder eines Computers ab. Stattdessen nimmt man also die Anzahl der dazu nötigen Arbeitsschritte als Maßeinheit.
Und außerdem interessiert einen nicht so sehr, wie viele Arbeitsschritte man für eine konkrete Aufgabe braucht (das Durchsuchen eines unsortierten Stapels von zwanzig Deutschklausuren nach der Arbeit eines bestimmten Schülers etwa), sondern wie viele Arbeitsschritte man für eine Aufgabe allgemein braucht (das Durchsuchen eines Stapels von Deutschklausuren nach einer Arbeit im Prinzip).
Wieviel Schritte man für das Durchsuchen eines Stapels von Deutschklausuren im Prinzip braucht, das hängt vor allem von einem ab: der Anzahl der Klausuren. Man braucht mehr Arbeitsschritte, wenn es mehr Klausuren sind. Und zwar ist es immer so, dass man bei einem doppelt so hohen unsortierten Klausurenstapel doppelt so viel Zeit braucht, um eine bestimmte Klausur zu finden. (Das gilt allerdings nur, wenn man nicht dem verbreiteten Glauben anhängt, dass es ohnehin immer die letzte Arbeit ist. Glückskinder könnten natürlich die gesuchte Arbeit immer als erste ziehen, deshalb interessiert uns hier vor allem der durchschnittliche Aufwand bei einer Aufgabe.)
Und dieser Aufwand – die Anzahl der Arbeitsschritte – wächst beim Durchsuchen eines Stapels linear. Das ist ein Fachausdruck für die Erscheinung „doppelt so viel Klausuren machen doppelt so viel Arbeit“ und heißt so, weil das eine lineare Funktion ist, die als Kurve so aussieht, nämlich gar nicht kurvig, sondern gerade: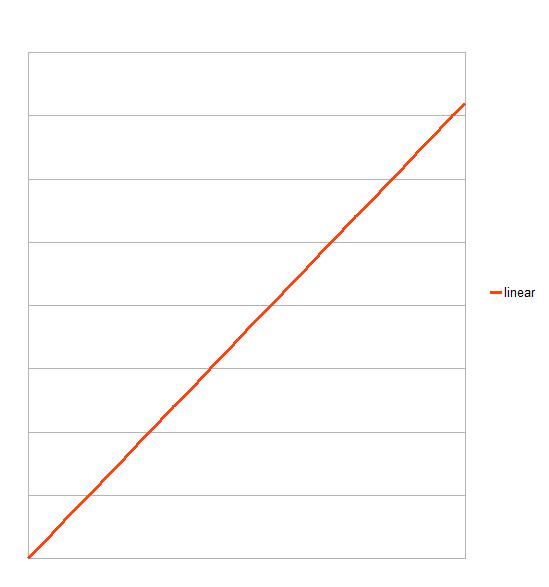
Die x-Achse enthält die wachsende Problemgröße (die Anzahl der Klausuren), an der y-Achse kann man den Aufwand ablesen. Es gibt absichtlich keine Einheiten, weil die uns ja nicht interessieren.
Jetzt könnte man argumentieren, das Bearbeiten einer Klausur seien in Wirklichkeit drei Arbeitsschritte, nämlich das In-die-Hand-Nehmen, das Lesen des Namens und das Ablegen auf einen Nachbarstapel. Das ändert aber nichts an dem Prinzip „doppelt so viel Klausuren machen doppelt so viel Arbeit“, die Kurve ist vielleicht etwas steiler, aber immer noch linear.
Und das gilt ungefähr auch noch, wenn man sich zehn Arbeitsschritte dafür anrechnet, den Stapel erst einmal aus der Schultasche zu ziehen, unabhängig von dessen Größe. Wenn es nur genügend Klausuren sind, spielt so ein einmaliger Zusatzaufwand, egal wie hoch er ist, keine große Rolle mehr. Wir in der Informatik sind da rechnerisch großzügig und pädagogisch pessimistisch und gehen von beliebig anwachsenden Klassengrößen aus.
Festgehalten: der Aufwand für das Durchsuchen eines unsortierten Klausurenstapels wächst linear (in diesem Fall: zur Anzahl der Klausuren).
Andere Aufgabenarten sind einfacher. Wenn ich beispielsweise einen Stapel von Deutsch-Schülerarbeiten zur Respizienz kriege, dann liegen obenauf zwei Kopien der Aufgabenstellung. Eine davon nehme ich und lege sie zur Seite, um sie – später mal – in einen Ordner zu tun. Dieser Aufwand ist für mich konstant, was die Anzahl der Arbeiten betrifft. Die Funktion dazu sieht so aus:
Ob man den Aufwand jetzt in einen oder drei oder zehn Arbeitsschritte zerlegt: er bleibt konstant (also unabhängig von der Anzahl der Klausuren).
Wir haben jetzt also schon Aufgaben mit konstantem Aufwand und welche mit linear wachsendem Aufwand. Der Aufwand kann aber auch noch schneller ansteigen, zum Beispiel beim Sortieren von Schüleraufsätzen. Da ist es nämlich so, dass das Sortieren von dreißig Aufsätzen nicht doppelt so viel Arbeit macht wie das Sortieren von fünfzehn, sondern mehr als doppelt so viel. (Aber: siehe unten.) Und bei einer Klasse von dreißig Schülern gibt es auch nicht doppelt so viele Chancen für Feindschaften, Tritte, Streit, Tratschereien, sondern mehr als doppelt so viel. Der Aufwand steigt mehr oder weniger quadratisch, und das sieht als Funktion so aus: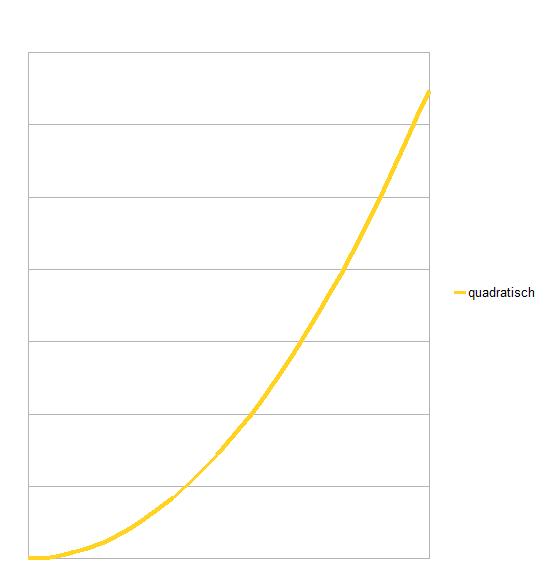
Beim Sortieren der Arbeiten hängt der Aufwand übrigens von der Sortiermethode ab. Nur bei den eher ungeschickten Methoden wächst der Aufwand quadratisch, bei anderen Methoden wächst er langsamer. Also sind die anderen Methoden in der Praxis sinnvoller. (In Wirklichkeit kommt bei Klausuren auch noch dazu, dass man ja weiß, dass die Arbeit von einer „Alexandra Abel“ wohl recht weit vorne zu liegen kommen wird, und die von „Zacharias Zuser“ ziemlich am Ende, selbst wenn man keine Ahnung hat, wie die Schüler in der Klasse sonst heißen. Und das erlaubt dann schon wieder noch schnellere Sortierstrategien.)
Festgehalten: Bei manchen Aufgaben steigt der Aufwand (abhängig von einer Eingangsgröße) quadratisch. Wir vernachlässigen wie oben schon andere konstante oder linear wachsende Arbeitsschritte, die eventuell noch dazu kommen – wenn die Zahl nur groß genug ist, läuft das auf quadratisch hinaus.
Ich stelle jetzt noch eine vierte Art von Aufgaben vor, bei der Art von Aufwand noch schneller wächst, nämlich exponentiell. Schon der quadratisch steigende Aufwand steigt ziemlich steil, aber der exponentiell steigende noch viel mehr, nämlich so: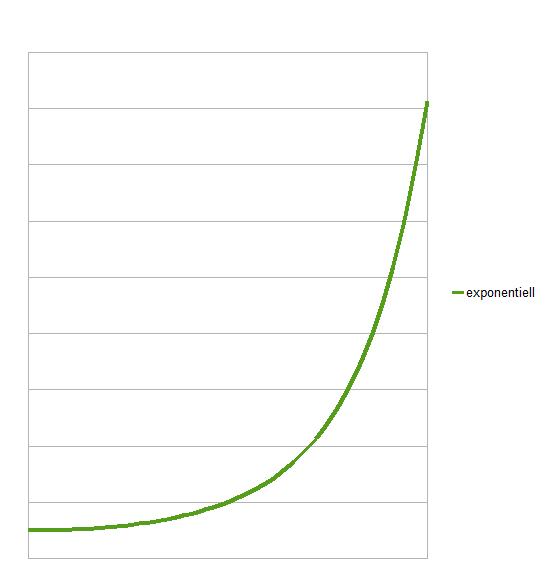
Wenn man zum Beispiel eine Zahl in Primfaktoren zerlegen möchte, dann steigt der Aufwand exponentiell zur Größe der Zahl. (Oder sagen wir: zumindest ist bisher keine bessere Lösung bekannt als eine mit exponentiell steigendem Aufwand. Wenn mal jemand eine finden sollte, wird der sehr berühmt werden.) Exponentielles Wachstum heißt: wenn eine Zahl x-mal so groß wird, dann ist der Aufwand für die Primfaktorzerlegung nicht etwa x-mal so groß (das wäre lineares Wachstum), und auch nicht x2-mal so groß (quadratisches Wachstum), sondern etwa 2x-mal so groß. Das klingt gar nicht so dramatisch, aber erinnern wir uns an die Sache mit den Reiskörnern auf dem Schachbrett. Im jeweils einfachsten Fall hat man bei linearem Wachstum am Schluss 64 Körner, bei quadratischem Wachstum 4096 Körner und bei exponentiellem Wachstum eine Zahl mit zwanzig Stellen.
Man sieht den Unterschied, wenn man alle vier Funktionen nebeneinander betrachtet: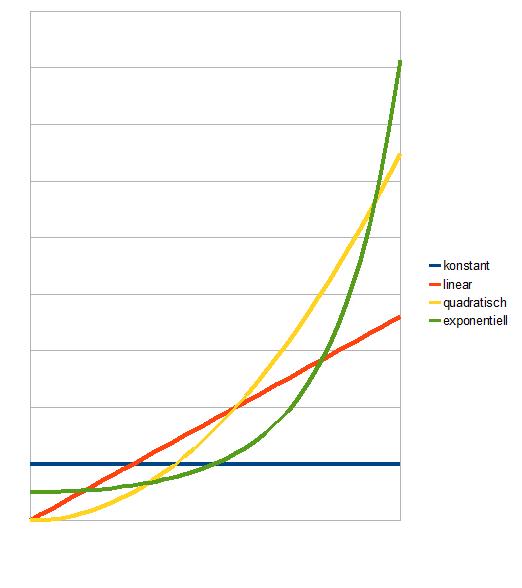
 Jede linear steigende Aufgabe wird irgendwann mal größer als jede konstante, jede quadratische überholt irgendwann mal die lineare, und die exponentiell steigende Kurve, selbst wenn sie mal langsam anfangen sollte, übersteigt irgendwann jede quadratische.
Jede linear steigende Aufgabe wird irgendwann mal größer als jede konstante, jede quadratische überholt irgendwann mal die lineare, und die exponentiell steigende Kurve, selbst wenn sie mal langsam anfangen sollte, übersteigt irgendwann jede quadratische.
Wenn die Grafik nur ein bisschen weiter nach rechts gehen würde, dann wäre die grüne Kurve sehr weit oben, und alle anderen, die gelbe eingeschlossen, so weit unten, dass man die Unterschied dazwischen nicht mehr gut erkennen könnte.
Exponentiell steigt schon sehr steil, aber es gibt natürlich auch noch steileres Wachstum, aber dazu vielleicht später mal. (Blogeintrag zur Ackermann-Funktion.)
— Als Zusammenfassung kommen jetzt ein paar mathematischer formulierte Beispiele für Steigungsverhalten. Dabei ist x jeweils die Eingangsgröße – Anzahl der Klausuren oder was auch immer. Dann ist f(x) der Aufwand in Arbeitsschritten, abhängig von dieser Eingangsgröße.
Konstant z.B.:
f(x) = 1
f(x) = 100
(Konstant ist etwa der Aufwand für das Suchen des kleinsten Elements in einer sortierten Liste.)
Linear z.B.:
f(x) = x
f(x) = 3*x
f(x) = 3*x + 100
(Linear wächst zum Beispiel der Aufwand für das Suchen in einer unsortierten Liste.)
Quadratisch z.B.:
f(x) = x2
f(x) = x2 + 100
f(x) = x2 + 3*x + 100
(Quadratisch wächst zum Beispiel der Aufwand für das Sortieren einer Liste, wenn man mit einem nicht besonders guten Sortierverfahren arbeitet.)
Polynomiell* z.B.:
f(x) = x4
f(x) = x4 + x3
f(x) = x4 + x3 + x2 + 3000*x + 9000
Exponentiell z.B.:
f(x) = 2x
f(x) = 20x
f(x) = 2x + x4 + x3 + x2 + 3000*x + 9000
(Exponentiell wächst zum Beispiel der Aufwand bei der Primfaktorzerlegung.)
*Polynomiell ist eine Art Überbegriff zu quadratisch: x2 ist polynomiell, und x3 auch und x5 auch und so weiter – also immer dann, wenn es um xirgendwasgrößer1 geht. Das kann quadratisch sein oder nicht, mit der dem Informatiker eigenen Großzügigkeit sagen wir polynomiell dazu und gut ist.
Schreibe einen Kommentar