Executive summary: Es gibt eine besondere Art von Fragen, die schwer zu beantworten sind, aber wenn man die Antwort hat, kann man relativ leicht überprüfen, ob sie auch wirklich stimmt.
(Fortsetzung vom letzten Mal.) Als grobe Faustregel – und wir sind ja hier nur am Groben interessiert – kann man sagen:
- alle Fragen, für die sich mit linear steigendem Aufwand eine Antwort finden lässt, sind in der Praxis gut beantwortbar (und bei konstantem Aufwand sowieso)
- alle Fragen, für die sich mit polynomiell steigendem Aufwand eine Antwort finden lässt, sind in der Praxis gut beantwortbar
- alle Fragen, für die sich nur mit exponentiell steigendem Aufwand eine Antwort finden lässt, sind in der Praxis nur schwer zu beantworten (allerdings gibt es für manche dieser Aufgaben schnellere Lösungsverfahren, die zwar nicht das perfekte, aber immerhin ein halbwegs brauchbares Ergebnis liefern)
Faustregel deshalb, weil eine exponentielle Lösung bei sehr kleinem Exponenten und kleinen Ausgangswerten schneller sein kann als eine polynomielle Lösung hoher Ordnung. Soll uns jetzt nicht kümmern.
Die Klasse aller Aufgaben mit höchstens polynomiell steigendem Aufwand für das Lösen einer Aufgabe nennt man P. Das schließt die ersten der drei Fälle oben ein. Aufgaben in P sind in der Praxis gut machbar, auch wenn P nicht für „Praxis“ steht, sondern für „polynomiell“. Typische Aufgaben in P sind das Sortieren und Durchsuchen von Listen und das Finden kürzester Wege auf einer Straßenkarte.
Und dann gibt es noch eine andere Klasse von Aufgaben, die heißt NP. Da sind die Aufgaben drin, für die man mit höchstens polynomiellem Aufwand überprüfen kann, ob eine Lösung die richtige ist, wenn man sie denn einmal hat. (Das schließt alle Aufgaben aus P mit ein.)
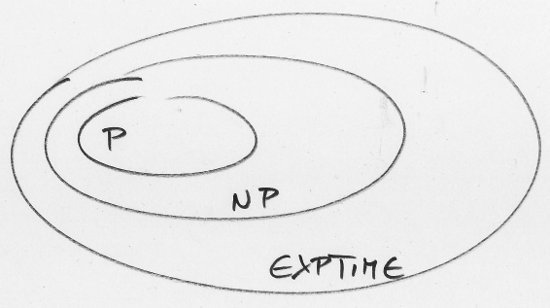
Daneben gibt es noch weitere Klassen, also zum Beispiel die Klasse EXPTIME. Da sind die Aufgaben drin, für die man mit höchstens exponentiellem Zeitaufwand eine Lösung finden kann. (Das schließt alle Aufgaben aus NP ein, und dann natürlich P sowieso. Aber dazu eben auch die Aufgaben, für die selbst das Überprüfen einer vorgeschlagenen Lösung sehr viel Arbeit macht.) Dazwischen und davor und dahinter und drumherum gibt es noch weitere Klassen, aber diese drei reichen uns hier. Ihr Verhältnis zueinander sieht man in diesem Diagramm:
Was gibt es denn für Aufgaben, die schwer zu lösen, aber relativ leicht oder auch sehr leicht zu überprüfen sind, also diejenigen Aufgaben, die in NP liegen, aber außerhalb von P?
Aus Im Laybrinth des Denkens von William Poundstone habe ich folgende schöne Idee. Da geht es um ein allwissendes Orakel, das beweisen soll, dass es allwissend ist. Man kann ihm solche Fragen stellen wie: „Was ist die zweibillionste Dezimalstelle von Pi?“, und es wird die Antwort ausspucken. Leider kann man die Antwort nicht so ohne Weiteres überprüfen, weil man das nirgendwo nachschlagen kann und das noch niemand ausgerechnet hat und das auch nicht so einfach auszurechnen ist – also wird die Antwort niemanden davon überzeugen, dass das Orakel wirklich allwissend ist.
Man kann das Orakel auch fragen: „Was ist die Quadratwurzel von 622521?“, und die Antwort wird ausgespuckt. Aber da könnten Zweifler sagen, dass das Orakel irgendwo einen Taschenrechner oder einen Spickzettel hat oder einfach ziemlich gut rechnen kann. Die Frage ist also zu leicht, als dass sie ein Beweis für die Allwissenheit des Orakel wäre.
Was man braucht, ist eine Frage, bei der es sehr, sehr schwer ist, die Antwort herauszufinden, selbst mit einem Taschenrechner oder Spickzettel oder Assistenten – aber wenn man sie einmal hat, kann man die Richtigkeit der Lösung schnell überprüfen. Und das sind eben die Aufgaben in NP, die außerhalb von P sind.
Dazu gehört zum Beispiel die Primfaktorenzerlegung. Es sieht auf den ersten Blick vielleicht nicht so aus, aber die Aufgabe, eine beliebige Zahl in Primfaktoren zu zerlegen, wächst exponentiell zur Größe der Zahl. Die fünfstellige Zahl 95477 in ihre zwei Primfaktoren zu zerlegen, das macht schon einigen Aufwand. Für einen Computer ist das aber noch leicht. Die doppelt so lange Zahl 3620188223 in ihre beiden Faktoren zu zerlegen, das macht aber nicht doppelt so viel Aufwand, und nicht zehnmal so viel Aufwand, sondern exponentiell mehr Aufwand. Und irgendwann, ab ein paar hundert Dezimalstellen, wird das auch für Computer praktisch nicht mehr berechenbar. Die Lösung zu überprüfen, das ist aber wieder einfach – das ist dann ja nur eine Multiplikation zweier Primzahlen.
Und mit diesen Primfaktoren funktioniert zumindest zum Teil auch die Verschlüsselung vieler Seiten und Nachrichten im Internet. Man schreit sozusagen heraus: „Huhu, ich habe hier ein seeeehr großes Produkt zweier Primzahlen. Dürft ihr euch alle anschauen, und wenn ihr die Zahl in ihre Faktoren zerlegen könnt, dann könnt ihr auch meine verschlüsselten Nachrichten lesen. Aber ellebätsch, das schafft ihr nicht!“
Mehr Beispiele für diese Art Aufgaben kommen im nächsten Teil dieser Eintragserie. Eigentlich gehören nur Fragen, die sich mit ja/nein beantworten lassen („Entscheidungsprobleme“) in die Kategorie P/NP; ich war beim Formulieren oben da nicht immer exakt.
Der Vollständigkeit halber: Was gibt es denn für Aufgaben, die schwer zu lösen sind (exponentieller Aufwand), und wo die Überprüfung ebenfalls schwer ist (exponentieller Aufwand)?
Ein richtig schönes Beispiel habe ich nicht gefunden. Wenn ein Schüler für n Vergehen 2n mal den Satz schreiben muss „Ich werde das nie wieder tun“, dann erfordert die Kontrolle, ob er seine Strafaufgabe gemacht hat, ebenfalls exponentiellen Aufwand (des Zählens). Vielleicht kommt hier irgendwann mal ein schöneres Beispiel hin.
Und zum Schluss und als Ausblick für eventuelle spätere Blogeinträge:
(1) Es gibt Aufgaben, die man nie berechnen können wird, weil man weiß, dass man das prinzipiell nicht berechnen kann. Zum Beispiel kann man kein Computerprogramm schreiben, dass zwei beliebige andere Programme unter allen Umständen und immer zum gleichen Ergebnis kommen.
(2) Es gibt Aufgaben, die man nie berechnen können wird, weil sie zwar eine Lösung haben, man das aber nie beweisen kann. Ein Beispiel dazu kann man nicht geben, weil, ja, weil man das ja nicht wissen kann.
(3) Es gibt Aufgaben, die garantiert eine Lösung haben, was man auch beweisen kann, die man aber nie wird berechnen können (Busy-Beaver-Funktion), weil – hm, das ist schwer zu erklären.
(Und insgesamt kürze ich ein ein bisschen ab. Mit Aufgaben meine ich immer: Fragen, und mit Lösungen: Antworten. Ist hier nicht so wichtig.)
Schreibe einen Kommentar