Executive summary: Die Fragen vom letzten Mal sind sich alle irgendwie ähnlich: Wenn man für eine davon einen effizienten Lösungsweg gefunden hat, kann man den auf die anderen übertragen. Wird man je einen finden?
Hier zur Erinnerung noch einmal der Ausschnitt aus den Komplexitätsklassen vom letzten Mal: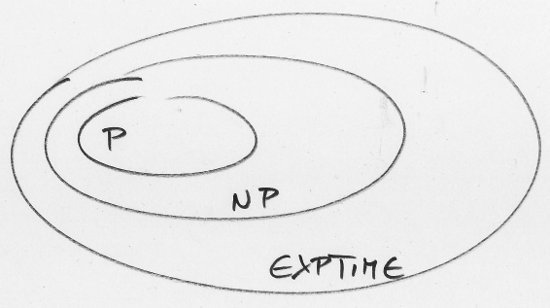
- In P, da liegen die relativ einfachen Aufgaben.
- In NP (aber außerhalb von P), da liegen die schweren Aufgaben, bei denen sich die Lösung wenigstens leicht überprüfen lässt. Die Zeichnung geht davon aus, dass P eine echte Teilmenge von NP ist, was nicht unbedingt stimmen muss.
- In EXPTIME (aber außerhalb von NP), da liegen die schweren Aufgaben, bei denen sich die Lösung auch nur schwer überprüfen lässt.
Der Handlungsreisende
Viele der Aufgaben aus (2) spielen in der Praxis eine große Rolle. Ein Beispiel dafür ist das Problem des Handlungsreisenden (Travelling Salesman). Das geht von einer Reihe von Orten aus, die zum Teil durch Straßen miteinander verbunden sind, etwa so:

Die Buchstaben stehen für die Ortsnamen, die Verbindungen dazwischen sind die Straßen. Das Ziel des Handlungsreisenden ist es, alle Orte zu besuchen, und zwar derart, dass er insgesamt möglichst wenig Entfernung zurücklegt und am Schluss wieder an seinem Ausgangspunkt ankommt. Die Aufgabe für ein Programm lautet etwa: Nenne mir eine solche Rundreise (wenn es sie denn gibt), die höchstens die Länge 9 hat. Wenn man erst einmal die Lösung hat, kann man recht einfach überprüfen, ob sie stimmt. Einfach heißt: in höchstens polynomieller Zeit. In diesem Beispielgraphen ist das sowieso sehr leicht. Dass es eine Lösung gibt, ist auch klar: zur Not probiert man einfach alle möglichen Kombinationen aus und schaut, ob eine geeignete dabei ist. Allerdings steigt der Aufwand dafür exponentiell mit der Anzahl an Orten und Verbindungen, wenn man eine allgemeine Lösungsweg hat. (Näherungsweise Lösungen gibt es sehr gute für dieses Problem.)
Die Freundesclique
Ein weiteres Beispiel für ein Problem aus (2) ist das Cliquenproblem. Da geht es um einen Haufen von Schülern, die sich mögen können oder nicht. Eine Clique ist dabei eine Gruppe von Schülern, von denen jeder jeden anderen in der Clique mag. Die Aufgabe dazu heißt: Nenne mir eine solche Clique (wenn es sie denn gibt), in der mindestens vier Schüler sind. Hier ist so ein Haufen von Schülern:

Die Buchstaben stehen für die Schüler (Anna, Bernd, Charlie, Denise…), die Verbindungen bedeuten, dass die sich mögen. Bei einer Handvoll Schüler geht das schnell, aber sobal die Zahlen größer werden, wird das aufwendiger: der Aufwand steigt nämlich exponentiell.
Die Antwort lautet übrigens: ja, es gibt eine 4er-Clique, nämlich {A, C, D, F}.
Logikrätsel
Auch Logikrätsel liegen in diesem Bereich. Damit meine ich beliebige Aufgaben wie
(x oder y) und (nicht (z) oder x)
Dabei sind x, y, z jeweils wahr oder falsch, und die Frage ist: gibt es eine Möglichkeit, dass diese logische Formel insgesamt wahr ist? Man kann das immer durch Ausprobieren aller Möglichkeiten überprüfen, aber bei n Variablen gibt es 2n Möglichkeiten, der Aufwand steigt exponentiell, und das ist nicht praktikabel.
Im Beispiel geht das noch, da kann man die 23=8 Möglichkeiten ausprobieren, und ja, es sind sogar 5 richtige dabei.
Zerlegung in Primfaktoren
Ein viertes Beispiel für ein Problem aus (2) ist die Primfaktorenzerlegung. Bei manchen Verschlüsselungstechniken nutzt man gerade das aus, dass diese Aufgabe so schwer ist – wäre sie es nicht, wäre das nicht sicher. (Zugegeben, ich kürze hier etwas ab – die NP-Probleme sind nämlich eigentlich Entscheidungsprobleme.)
Ähnlichkeit all dieser Aufgaben
Der Knackpunkt ist jetzt der, dass die verschiedene Aufgaben in (2) sich ähnlicher sind, als man meint, und das in zweierlei Hinsicht.
- Erst mal hat man für keine davon allgemeinen Lösungen in polynomieller Zeit gefunden, sondern nur welche mit exponentiellem Aufwand. Das heißt aber nicht, dass es keine schnelleren Lösungen gibt! Vielleicht findet man ja noch welche.
- Zweitens sind sie sich so ähnlich, dass, wenn man für eines davon eine solche effizientere Lösung gefunden hat, diese Lösung auch für alle anderen gilt. Und das ist das eigentlich Interessante an diesen Aufgaben, aber dazu werde ich kurz etwas ausholen.
- Wenn man sicher sein wollte, dass es keine solche effiziente Lösung gibt, dann müsste man beweisen, dass es Probleme gibt, die in NP liegen, aber nicht in P – anders gesagt, dass P ungleich NP. Das ist das P=NP-Problem. Und das konnte noch keiner beweisen oder widerlegen. Wer’s tut, dem winken eine Million Dollar. So viel ist für die Lösung eines der Millenium-Probleme ausgesetzt. Man geht davon aus, dass P tatsächlich ungleich NP ist, dass man also nie eine effiziente Lösung finden wird.
— Wer jetzt noch dabei ist, verträgt ein paar Definitionen:
Zurückführen auf einen anderen Aufgabentyp (Reduktion)
Nehmen wir an, ich wäre bereits in der Lage, zwei beliebige Zahlen miteinander zu multiplizieren.
Dann bin ich auch in der Lage, Quadratzahlen zu berechnen.
Denn das Quadrieren einer Zahl lässt sich auf das Multiplizieren zweier Zahlen reduzieren. (Ich muss nur zusätzlich darauf achten, dass die beiden Faktoren gleich sind.)
Wenn der zusätzliche Aufwand bei der Reduktion vertretbar, also höchstens polynomiell ist, heißt das polynomielle Reduktion.
Genau genommen gilt das für die Reduktion und P und NP nur für formale Sprachen und Entscheidungsprobleme und nicht für meine meist salopp formulierten Aufgaben. Aber ich lasse das jetzt alles mal so stehen.
Wenn ich Problem A auf Problem B in vertretbarer Zeit zurückführen kann, und ich eine vertretbar schnelle Lösung für Problem B habe, dann kann ich auch Problem A in vertretbarer Zeit lösen.
NP-schwer/NP-hart
Ein Problem ist NP-schwer, wenn ich jedes Problem aus NP in polynomieller Zeit darauf zurückführen kann, insbesondere natürlich die besonders schwierigen. Ein NP-schweres Problem kann also selber in NP (aber gleichzeitig nie in P) liegen. Es kann aber noch schwerer sein, also zum Beispiel echt in EXPTIME liegen.
NP-vollständig
Ein Problem ist NP-vollständig, wenn es erstens in NP liegt, also wenn die Lösung in polynomieller Zeit auf Richtigkeit überprüft werden kann.
Und zweitens muss jedes andere Problem in NP (also insbesondere die schwierigen davon) mit polynomiellem Aufwand darauf zurückführbar sein. Ein NP-vollständiges Problem liegt also in NP und ist NP-schwer.
Alle Aufgaben oben sind NP-vollständig.
Beweise
Dass ein Problem NP-vollständig ist, erforderte zuerst einmal viel Beweisaufwand. Aber wenn man erst einmal ein solches Problem gefunden hat, dann lässt sich das mit weniger Aufwand für weitere beweisen. Wenn ich das Problem des Handlungsreisenden polynomiell reduzieren kann auf das Problem des ungerichteten Hamilton-Kreises, und wenn ich weiß, dass das NP-vollständig ist, dann ist auch der Handlungsreisende NP-vollständig.
Und das mit dem Hamilton-Kreis weiß ich, weil man den auf einen gerichteten Hamilton-Kreis polynomiell reduzieren kann, von dem man weiß, dass er NP-vollständig ist.
Und das weiß man, weil man den auf das Problem 3KNF-SAT polynomiell reduzieren kann, von dem man weiß, dass es NP-vollständig ist.
Und das weiß man, weil man es auf das Problem SAT polynomiell reduzieren kann, von dem man weiß, dass es NP-vollständig ist.
Und das weiß man – weil es mal bewiesen wurde.
Zusammenfassung
Jedes NP-vollständige Problem auf jedes andere NP-vollständige Problem polynomiell reduzieren. Das heißt, wenn man für ein Problem in NP einen effizienten (polynomiellen, nicht exponentiellen) Lösungsweg gefunden hat, dann kann man plötzlich alle Probleme in NP in polynomieller Zeit lösen, weil zur ursprünglichen Lösung dann allenfalls noch polynomieller Reduktionsaufwand hinzukommt.
Deswegen wäre es so wichtig, zu wissen, ob P=NP oder nicht. Wenn nicht, dann ist klar, dass es nie eine effiziente Lösung für irgendein NP-vollständiges Problem geben wird. (Für Spezialfälle und Näherungen natürlich schon.) Davon geht man aus, dass also P ungleich NP. Aber bewiesen ist es halt noch nicht.
Beispiel
Dazu ein Beispiel aus dem Staatsexamen Informatik, Frühjahr 2007, Theoretische Informatik, Thema 2, Aufgabe 4:
Das Partyveranstaltungsproblem ist das folgende. Gegeben ist eine Menge B von Bekannten und eine Menge H ⊆ B × B von (Paaren von) Bekannten, die sich nicht leiden können. Es ist festzustellen, ob eine Auswahl U ⊆ B von k Bekannten (|U| = k) existiert (die Gästeliste), sodass in dieser keine zwei Bekannten enthalten sind, die sich nicht leiden können. Man zeige, dass das Partyveranstaltungsproblem NP-vollständig ist.
Dass das Partyproblem NP-vollständig ist, beweist man so:
Man beweist erstens, dass es in NP ist und zweitens, dass es in polynomieller Zeit auf ein NP-hartes Problem zurückgeführt werden kann – zum Beispiel auf ein bereits bekanntes anderes NP-vollständiges Problem. Dann ist es selber NP-vollständig. Und da gibt es eines, das heißt Independent Set-Problem und ist eigentlich das gleiche wie das Party-Problem.
Fußnote
Wissenschaftler des Queen Mary and Westfield College der Universität London fanden heraus, dass Hummeln bei der Nahrungssuche in der Lage sind, das Problem des Handlungsreisenden besser und effizienter zu lösen, als dies mit den bislang bekannten mathematischen Computerverfahren möglich ist. Wie Hummeln diese Ergebnisse erzielen können, ist dabei noch nicht geklärt.
Schreibe einen Kommentar