Monat: Mai 2013
-

Für die Nachbarn, und so
(7 Kommentare.) Ich habe eine neue Ukulele, und zwar eine elektrische. Also nicht nur mit Tonabnehmer, dass man sie verstärken kann, sondern nur damit, und ganz ohne Klangkörper. Der Vorteil: Die Ukulele ist unverstärkt so leise, dass ich auch nachts damit üben kann und auch Frau Rau damit weniger auf die Nerven falle. Rocktile Frame…
-
Informatik als Schulfach?
(9 Kommentare.) Der Haltungsturner beklagt, dass seine Kinder kein Schulfach Informatik haben. Er hält Smartboards und Tablets und Suchstrategien im Web für wichtig und wünscht sich mehr davon, bemerkt aber, dass das nichts mit Informatikunterricht zu tun hat. Manche der Kommentatoren dort, wenn ich sie denn recht verstanden habe, sehen eher die Notwendigkeit für eine…
-

Der Digi-Comp II
(8 Kommentare.) Unsere Fachschaft Informatik hat sich – mit Geld vom Elternbeirat – den Digi-Comp II gekauft: Das ist ein Computer, ganz aus Holz. Also gut: Es ist kein Computer, sondern ein Rechner, der vor allem multiplizieren und addieren kann. Aber das mit dem Holz stimmt. Betrieben wird er mit kleinen Metallmurmeln. Im Prinzip kann…
-

Wie viel Programmieren muss ich für die Oberstufe können?
(14 Kommentare.) Eigentlich geht es in der Informatik gar nicht so ums Programmieren. Auch in der Schule nicht. Aber wenn man nicht programmieren kann, macht einem die Oberstufe keinen Spaß – ob man eine Algorithmus verstanden hat, zeigt sich oft erst beim Programmieren, und wenn man die Konzepte, die man so lernt, ausprobieren möchte, kommt…
-
Ankündigung
In vier Wochen gibt es an meiner Schule einen Vortrag für Eltern und Lehrer und interessierte Schüler zum Thema „ethische Perspektiven für das Mitmachnetz. Dabei geht es u. a. um die Gefahren des Internets.“ Kostet 3 Euro. Ich glaube, da werde ich hingehen.
-
Anlässlich meiner ersten Abituraufsicht im Fach Musik heute
(9 Kommentare.) These, über die ich noch nicht viel nachgedacht habe: Ich finde die Art Allgemeinbildung, die einen in die Lage versetzt, dass man die Fragen in Abituraufgaben in den verschiedenen Fächern verstehen und einordnen kann, ziemlich ausreichend. Zu dieser Allgemeinbildung müssen natürlich noch andere Techniken kommen (schreiben, erklären, recherchieren). (Musikabitur: Ist ein echtes Gerenne.…
-
Ray Harryhausen
(5 Kommentare.) Vorgestern ist Ray Harryhausen mit 92 Jahren gestorben. Frau Rau meinte, ich soll etwas über ihn schreiben, weil sie noch nie jemanden über ihn hat reden hören außer mich. Wenn man sagt, dass Harryhausen ein Hollywood-Tricktechniker der 1950er und 1960er Jahre war, dann reicht das nicht. Er prägte die Fantasy- und Abenteuerfilme seiner…
-

Abitur, Berufsinfomessen, Krimskrams
(13 Kommentare.) Diese Woche: Elternsprechabend, angenehm und entspannt. Keine schwierigen Themen diesmal. Dann war da noch die Einschreibung für zukünftige Fünftklässler – immer wieder spannend: mehr Schüler, weniger Schüler, mehr mit Probeunterricht oder weniger? (Probeunterricht: An dem kann jeder Grundschüler teilnehmen, egal was er für Noten hat. Wer den besteht, kann auch ohne Gymnasialempfehlung aufs…
-
Mein kleines dunkles Geheimnis
(2 Kommentare.) Auf meinem Rechner befinden sich mehrere mit dem Programm TrueCrypt verschlüsselte Dateien. Sie sind jeweils 4 GB groß, so dass ich sie noch auf meinen handelsüblich formatierten USB-Stick packen kann. TrueCrypt funktioniert so: Nach dem Starten von Windows werde ich um ein Passwort gebeten, und wenn ich das richtige eingebe, wird zum Beispiel…
-
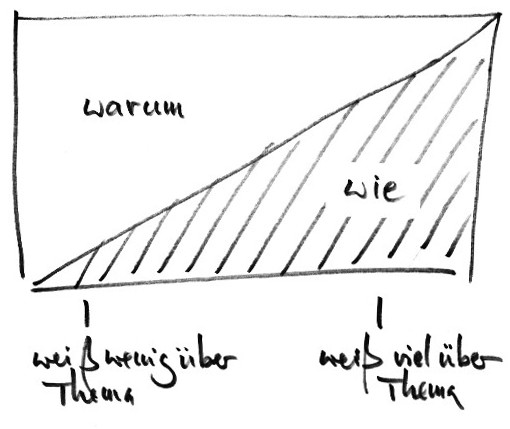
Sachen erklären können: The Art of Explanation
(12 Kommentare.) Dinge erklären können gehört, ob man das gut findet oder nicht, zum Lehrersein. Was heißt das, etwas erklären, und wie macht man das gut? Lee LeFever kennt man von seiner Firma Commoncraft – die machen Erklärvideos „in plain English“, wie etwa das hier: Bekannt geworden ist Commoncraft vor einigen Jahren durch „Wikis in…