(Fortsetzung von hier.)

Mit Reinforcement Learning kann sich eine selbständig agierende KI, auch Agent genannt, zum Beispiel beibringen, ein Spiel zu spielen, Pacman oder Space Invaders oder Pong oder Super Mario World oder ein Autorennspiel, oder gleich Auto zu fahren. Die Schwierigkeiten werden dabei allerdings immer größer, und für die Schule wird man sich auf einfache Fälle beschränken müssen.

Ich will mich dem Konzept in zwei Schrittten nähern. In diesem Blogeintrag geht es um den ersten davon: Aufschreiben, welche Entscheidungen direkt zu Erfolg und welche direkt zu Misserfolg geführt haben. Später dann die erfolgreichen verwenden, duh! Auch wenn dieser Blogeintrag sehr lang ist, geht es gar nicht um mehr als das; ich zeige das nur an etlichen Beispielen.

Das Prinzip ist noch ganz einfach: Wenn eine Entscheidung in einer bestimmten Situation zu Erfolg, zum Beispiel Sieg in einem Spiel, geführt hat, merke ich mir das. Und wenn sie in einer bestimmten Situation zu Misserfolg, einer Niederlage in einem Spiel, geführt hat, merke ich mir das auch, Das Merken geschieht in einer Tabelle, die Q-Tabelle heißt. Das Q steht für Qualität, weil in der Tabelle die Qualität der Entscheidungen festgehalten wird, die Wertigkeit.

Beispiel 1: Mau-Mau

Spielerin 1 denkt sich eine Ablageregel für Spielkarten aus, zum Beispiel eine vereinfachte Mau-Mau-Regel: man darf immer ablegen, wenn die eigene Karte den gleichen Wert oder die gleiche Farbe hat, sonst nicht. Spielerin 1 legt eine zufällige Karte ab, der Agent (Spieler 2) soll die geheime Regel herausfinden oder jedenfalls alle Karten legal zu spielen. Beim induktiven Kartenspiel Eleusis, hier oft genug thematisiert, geht es übrigens genau darum, dass eine Person sich eine solche Regel ausdenkt und die anderen versuchen müssen, ihre Karten passend auszuspielen.

Nun schreibt man ein Programm, dass den Agenten ein paar Runden spielen lässt und alles mögliche ausprobieren lässt. Er soll am Anfang wirklich zufällig Karten auswählen und sich merken, ob der Zug gut war oder nicht. Wenn der Agent eine gültige Karte ausgewählt hat, trägt er sich das in eine Tabelle ein, und wenn der Agent eine ungültige Karte gespielt hat, ebenfalls. Schon recht bald hat sich der Agent diese Tabelle angelegt, wobei in der ersten Spalte jeweils der vorgefundene Zustand steht, also die oben liegende Karte, und in den folgenden Spalten die möglichen Spieloptionen:

	♥A	♥2	♥3	♠A	♠2	♠3
♥A	gut	gut	gut	gut	nicht gut	nicht gut
♥2	gut	gut	gut	nicht gut	gut	nicht gut
♥3	gut	gut	gut	nicht gut	nicht gut	gut
♠A	gut	nicht gut	nicht gut	gut	gut	gut
♠2	nicht gut	gut	nicht gut	gut	gut	gut
♠3	nicht gut	nicht gut	gut	gut	gut	gut

Wenn die Tabelle auf Basis der Rückmeldungen erstellt worden ist, wird der Agent keine falsche Karte mehr spielen. Kann man sagen, dass der Agent die geheime Regel kennt? Vermutlich nicht. Das System funktioniert natürlich auch bei beliebig komplizierten Ablageregeln, sofern die nur von der oben liegenden Karte abhängen. Das Spiel Eleusis wird dadurch spannend, dass man nur eine begrenzte Anzahl an Versuchen hat, auf die Regel zu kommen, weil das durch schlichtes Ausprobieren ja sonst leicht ist.

Neu eingeführt in diesem Beispiel: Die Q-Tabelle.

Ausblick auf ein späteres Problem: Wenn der Agent gerade noch am Lernen ist und die Tabelle so weit aufgebaut hat:

	♥A	♥2	♥3	♠A	♠2	♠3
♥A	gut	gut	gut	gut	nicht gut	nicht gut
♥2	gut			nicht gut	gut

und wenn dann eine ♥2 oben liegt, was soll der Agent dann machen? Sicher nicht die als „nicht gut“ überprüften und verworfenen Züge, aber soll er die unbekannten ausprobieren oder sich auf die bereits gefundenen Lösungen verlassen? Bei diesem einfachen Spiel macht das keinen großen Unterschied, später wird das aber wichtiger werden. Exploration heißt das Verhalten, auch mal riskantere Dinge auszuprobieren. Im Moment probiert unser Agent einfach willkürlich alles aus, und wenn er fertig trainiert ist, nimmt er eine der guten Möglichkeiten.

Beispiel 2: Monty Hall/Das Ziegenproblem

Dieses Beispiel ist benannt nach dem Gastgeber und Produzenten der Show Let‘s Make A Deal. (Auf Deutsch heißt das Äquivalent Ziegenproblem, zuerst begegnet bei Gero von Randow.) Es gibt in der Show 3 geschlossene Türen, hinter einer ist der zu gewinnende Preis. Der Kandidat oder die Kandidatin wählt zuerst eine Tür, Monty Hall öffnet eine andere Tür, hinter der garantiert kein Preis ist. (Das geht, weil Monty weiß, wo der Preis ist.) Danach bietet Monty an, die Entscheidung zu wechseln auf die andere weiterhin geschlossene Tür. Soll man wechseln, soll man nicht wechseln, oder spielt es keine Rolle?

Die Lösung herauszufinden ist für einen Menschen wohl nicht ganz einfach, deshalb wird dieses Problem auch gerne als Denksportaufgabe oder in Büchern über Intuition und Wahrscheinlichkeit verwendet. Wenn man sich länger damit beschäftigt oder das mal selbst programmiert hat, verschwindet die Verwirrung. Ich möchte das als nächstes Beispiel verwenden, eben weil die Lösung nicht ganz so offensichtlich ist.

Neu sind aber zwei Dinge. Erstens, das Spiel besteht jetzt aus zwei Zügen. In Zug 1 entscheidet man sich für Tür 1, 2 oder 3, in Zug 2 entscheidet man sich für oder gegen einen Wechsel zur von Monty angebotenen Tür. Nur der zweite Zug spielt eine Rolle, der erste ist völlig egal, deshalb ist dieser Unterschied hier nicht wichtig. Zweitens jedoch ist das Spiel jetzt nicht mehr deterministisch. Egal ob sich der Wechsel von der Wahrscheinlichkeit her lohnt oder nicht, man kann mit jeder Entscheidung gewinnen oder verlieren. Ein bloßes gut/nicht gut in der Q-Tabelle reicht also nicht. Wir schreiben stattdessen in die Tabelle die Anzahl der Erfolgsfälle, zählen also schlicht mit, wie oft in einem bestimmten Spiel-Zustand die Entscheidung zu Erfolg geführt hat oder nicht. Der Spielzustand ist hier zum Beispiel mit dem kryptischen ?-1-2-0 notiert. Das ist so zu lesen: ? ist die unbekannte Gewinntür, die erste 1 die erste Entscheidung der Kandidatin, die 2 das Wechselangebot von Monty, und die letzte Ziffer die endgültige Entscheidung der Kandidatin – hier eben noch nicht ausgeführt. Bei 1000 Zufallsdurchgängen kamen folgende Häufigkeiten von zum Gewinn führenden Zügen heraus:

Zustand	Tür 1	Tür 2	Tür 3
?-1-2-0	26.0	50.0	x
?-1-3-0	26.0	x	46.0
?-2-1-0	60.0	36.0	x
?-2-3-0	x	17.0	46.0
?-3-1-0	50.0	x	27.0
?-3-2-0	x	59.0	26.0

Man sieht: In jeder Zeile gibt es eine Entscheidung, die etwa doppelt so oft zu einem Gewinn geführt hat. Mehr weiß die Tabelle auch nicht, der trainierte Agent wählt am Ende halt immer das mit der höchsten Wertung aus. Nur der Mensch kann das Muster dahinter erkennen: Wechseln erhöht die Chance auf einen Sieg immer!

Dafür brauche ich eigentlich kein Reinforcement Learning, das kann ich auch durch einfaches zufälliges Ausprobieren und Mitzählen herauskriegen. Aber ist nicht genau das, was unser Reinforcement Learning bis jetzt ohnehin ist?

(Fußnote zur Programmierung, weil ich das erst später gemerkt habe: Wenn auch Monty Hall durch einen zustandabhängigen Agenten gespielt wird, müssen für den andere Zustände ausgegeben werden als für den Kandidaten.)

Neu eingeführt in diesem Beispiel: In der Q-Tabelle stehen jetzt Zahlenwerte, die sich ändern können. Das ist hier nötig, weil das Spiel ein Zufallselement enthält, Das eröffnet später aber auch bei deterministischen Spielen neue Möglichkeiten, deshalb bleiben wir dabei.

Beispiel 3: Schlag den Roboter

Dieses Beispiel wird in der Informatikdidaktik viel verwendet: Das kann man schön mit farbigen Schokolinsen und enaktiv umsetzen. Hier verwende ich das Material von Stefan Seegerer dazu, verlinkt ganz unten.

Das Spiel ist eine Art Mini-Schach auf einem 3×3-Spielfeld, mit drei Bauern auf jeder Seite. Oben die Affen der menschlichen Spielerin, unten die Roboter (oder, in anderen Fassungen, Krokodile) des KI-Agenten.

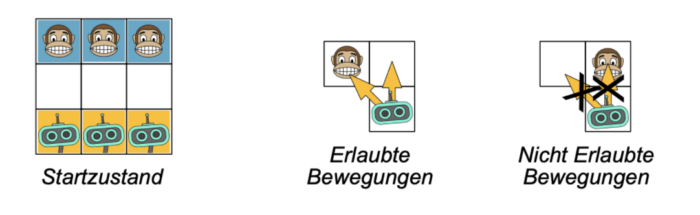
Gezogen wird wie im Schach, gewonnen hat man, wenn man (1) die gegenüberliegende Seite mit einer Figur erreicht hat oder (2) alle gegnerischen Figuren geschlagen hat oder (3) der Gegner keinen Zug mehr machen kann,

Die menschliche Spielerin 1 beginnt immer mit einem Zug der Affen. Der Agent ist immer Spieler 2, der mit den Robotern oder Krokodilen. Bei optimaler Strategie gewinnt Spieler 2 immer. Das ist am Anfang aber noch nicht offensichtlich, etwa wenn sich Schülerinnen und Schüler enaktiv als KI-Agent versuchen, dem Schokolinsen-Algorithmus folgend.

Es insgesamt 37 verschiedene Spielzustände, denen der Agent begegnen kann, wovon 18 spiegelsymmetrische Varianten anderer Zustände sind. Am Ende sollte der Agent also eine Tabelle mit 37 gefüllten Zeilen erstellt haben. Zugmöglichkeiten gibt es mehr, nämlich in meiner Schreibweise 14, wobei nicht alle Züge in jedem Spielzustand legal möglich sind; je nach Zustand stehen nämlich maximal 4 zur Auswahl, meist sind es 2 oder 3. Wenn man eine Q-Tabelle verwendet, braucht man also 14 Spalten für die Werte.

Wenn der Agent in einem dieser Zustände einen Zug ausprobiert, und danach gewonnen hat, wird der Wert in der Q-Tabelle für diesen Zug um eins heraufgesetzt. (Eine zusätzliche Schokolinse inder Farbe des Zuges hingelegt.) Wenn der Agent in einem dieser Zustände ausprobiert und nach dem Zug von Spielerin 1 verloren hat, wird der entsprechende Wert in der Q-Tabelle um eins verringert. (Eine Schokolinse der passenden Farbe entfernt, etwa durch Aufessen.) Der Startwert für jeden Eintrag in der Q-Tabelle beträgt, anders als beim vorherigen Beispiel 1 – letztlich weil man nur dann mit Schokolinsen arbeiten kann.

Wenn der Agent mit seinem Zug weder unmittelbar gewonnen noch verloren hat, ändert sich am Q-Wert in der Tabelle nichts. (Ein Ausblick: Das wird sich im nächsten Blogeintrag ändern.)

Wenn man den Agenten 100000 mal gegen eine Zufallsspielerin spielen lässt, ist danach eine Q-Tabelle entstanden, die für jeden Zustand und jeden in diesem Zustand möglichen Zug Buch geführt hat, wie oft der Zug zu einem Sieg oder einer Niederlage geführt hat und wie oft nicht.

Schauen wir uns ein paar Zustände an, hier der, den ich willkürlich Zustand 1 genannt gabe, und zwar mit der Bewertung der Züge am Anfang des Spiels. Es gibt drei mögliche Züge für Agent/Roboter/Krokodil, alle mit einem Schokoteil gleich hoch bewertet:

Nach ein paar Runden hat sich die Bewertung aber geändert. Man liest das so: 1 bedeutet einen Affen, 2 ein Krokodil oder einen Roboter, Move 63 bedeutet einen Zug von Zelle 6 nach Zelle 3. Die Zellen sind nummeriert von links oben 0 bis rechts unten 8.

1      1|1|0     Move 63 (-3750.0)
       0|0|1     Move 74 (-5645.0)
       2|2|2     Move 75 (1.0) 

In Schokoladenschreibweise:

Die drei möglichen Züge für den Agenten haben jetzt teilweise andere Werte. 7-4, also von unten mittig nach Mitte, hat einen negativen Wert; kein Wunder, mit diesem Zug verliert der Agent anschließend in einem von zwei möglichen Fällen, weil Spielerin 1 einen Siegzug machen kann. Bei vielen Wahlen dieses Zuges wurde der Q-Wert beziehungsweise die Anzahl der Schokolinsen der entsprechenden Farbe um 1 verringert. (Es sind keine mehr da.) Der Wert von 6-3, also von unten links nach mittig links, ist ebenfalls niedrig, weil Spielerin 1 danach drei Optionen hat, von denen eine zur unmittelbaren Niederlage für den Agenten führt. Der Wert ist also oft verringert worden, aber nicht immer; erhöht wurde er nie, weil er nie zu einem unmittelbaren Sieg führt. (Schokolinsen sind keine mehr da.) Und der Zug 7-5 hat noch die ursprüngliche Bewertung, da er weder unmittelbar zu einem Sieg führt noch unmittelbar zu einer Niederlage führen kann. (Die eine Schokolinse vom Anfang liegt weiter da.)

Ähnlich ist Zustand 4:

4      1|0|0     Move 74 (-572.0)
       1|0|1     Move 73 (1192.0)
       0|2|2     Move 75 (-1253.0) 

In dieser Situation gibt es drei legale Züge, 7-3 ist hoch bewertet, er führt ja auch zum unmittelbaren Sieg. (Spielerin 1 kann dann nicht mehr ziehen.) 7-5 ist sehr niedrig bewertet, er führt stets zur Niederlage. (Spielerin 1 kann dann nur einen Zug machen, einen Gewinnzug.) Und 7-4 ist nicht ganz so niedrig bewertet, er führt nicht automatisch, aber eben doch mit einer Chance von 50% zu einem unmittelbaren. Gewinnzug von Spielerin 1. (Im Schokolinsenmodell ist 7-3 heraufgesetzt, die anderen Züge haben keine Linsen mehr; der Unterschied zwischen 7-4 und 7-5 kann mit den Schokolinsen nicht modelliert werden.)

Auf andere Art interessant ist Zustand 34:

34     0|0|0     Move 84 (-1212.0)
       1|1|1
       0|0|2 

Alle Möglichkeiten (okay, es gibt nur eine) haben einen stark negativen Wert. Das heißt, in diesem Zustand gibt es keine Möglichkeit mehr, zu gewinnen. Es müsste also eigentlich Folgendes geschehen: Der vorhergehende Zug des Agenten, der dazu führt, dass Spielerin 1 den Agenten mit ihrem Zug überhaupt erst in diese blöde Situation Nummer 34 bringen kann, müsste negativ bewertet sein. Aber das geht nicht, weil ja nur unmittelbare Sieg- oder Niederlage-Züge bewertet werden und nicht mittelbare.

Ein solcher Zustand, der theoretisch zu Nummer 34 führen kann, ist Nummer 13:

13     0|1|0     Move 64 (-1875.0)
       1|1|0     Move 85 (-1222.0)
       2|0|2     Move 84 (1899.0) 

Der bietet Move 8-4, der zu unmittelbarem Sieg führt (Spielerin 1 kann dann nicht mehr ziehen und verliert deswegen); Move 6-4, der zu unmittelbarer Niederlage führt (Spielerin 1 hat dann nur eine legale Zugmöglichkeit, die ihr dann den Gewinn bringt); und Move 8-5, der deshalb niedrig bepunktet ist, weil er zu unmittelbarer Niederlage führen kann, und nicht deshalb, weil er auch im anderen Fall im übernächsten Zug garantiert zur Niederlage in Form von Zustand 34 führen wird. Im Idealfall hätte 8-5 einen ähnlich hohen Negativwert wie 6-4, weil er ebenso alternativlos zu einer Niederlage führt, nur halt teilweise erst später. – Im Minischach spielt das keine große Rolle, weil alle Züge, die zu Nummer 34 führen können, aus anderen Gründen niedrig bewertet sind. Im nächsten Beispiel wird das schon anders sein.

Mein kleiner Vorbehalt gegenüber der enaktiven Schokolinsenversion: Man vollzieht dabei Schritt für Schritt nach, was der Algorithmus macht, hat aber vielleicht keinen Blick auf das Prinzip dahinter: alles ausprobieren, sich Gewinn- und vor allem Niederlagenzüge merken und das beim nächsten Mal im gleichen Zustand berücksichtigen.

Neu eingeführt in diesem Beispiel: Ein erster Hinweis darauf, dass Sackgassen-Züge nicht erkannt werden, also Züge, die mittelbar immer zu einer Niederlage führen.

Beispiel 4: Tic-Tac-Toe

Bei diesem Beispiel wird das Problem, das im Minischach noch wenig wichtig war, deutlicher. Tic-Tac-Toe, das ist das hier:

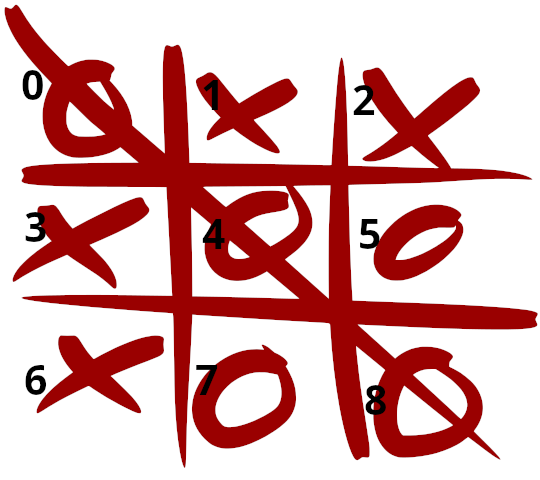
Die neun bespielbaren Kästchen habe ich wieder von 0 bis 8 durchnummeriert. Eine „1“ in einem Kästchen bedeutet Spielerin 1, eine „2“ Spieler 2, eine „0“, dass es leer ist. Die gezeichnete Situation oben sieht für den Rechner also eher so aus wie das hier:

1|2|2
2|1|1
2|2|1

Bei diesem Spiel soll der Agent lernen, vor dem Menschen drei in eine Reihe zu bringen. Das Prinzip ist wieder das gleiche: Aus allen legalen Zügen wählt der Agent erst einmal willkürlich einen aus; wenn der Agent danach gewonnen hat, gut; wenn er verloren hat, nicht gut. Es gibt jetzt allerdings viel mehr zu berücksichtigende Zustände, nämlich 2097 – 9 davon mit 8 Zugmöglichkeiten (nämlich der erste Zug des Agenten in der Rolle von Spieler 2), die anderen 7 bis 1. Viele davon sind symmetrische Varianten anderer Zustände. Das kann man nicht mehr gut in einer Tabelle aufschreiben, aber für einen Computer ist die Verwaltung solch einer Tabelle immer noch sehr leicht.

Der Startwert für jeden Zug ist wieder 1,0 wie im letzten Beispiel. Ohne Schokolinsenzählung wäre ein Startwert von 0,0 naheliegender, so wie bei Monty Hall übrigens, aber ich habe das mal so gelassen, der Einfachheit halber.

Wenn man den Agenten 200000 mal Tic-Tac-Toe gehen Zufallsspielerin 1 spielen lässt (weniger wäre sicher auch okay), dann kommt am Ende eine Q-Tabelle heraus, die aus Zeilen wie dieser besteht, hier lesbar aufbereitet:

0|0|0     Move 0 (-15.0)
1|2|2     Move 1 (-13.0)
0|1|1     Move 2 (-5.0)
          Move 6 (1.0)

Das liest man wieder so: Beim angegebenen Spielstand hat Move 0 (eine 2 links oben setzen) den Wert -15, Move 1 (eine 2 oben mittig) den Wert -13, auch Move 2 (oben rechts) ist negativ. Das liegt jeweils daran, dass diese Züge öfter zu einer unmittelbaren Niederlage als zu einem unmittelbaren Sieg geführt haben. Genauer gesagt, sie haben niemals zu einem unmittelbaren Sieg geführt, und manchmal zu einer unmittelbaren Niederlage. Nur manchmal, weil die Zufallsspielerin 1 ja manchmal übersieht, dass sie eine Siegmöglichkeit hat. Move 6 dagegen hat eine Quality von 1,0, das ist der unveränderte Startwert, weil dieser Zug nie zu einem unmittelbaren Sieg oder einer unmittelbaren Niederlage geführt hat. Kann er ja auch gar nicht.

Ein zweiter Tabelleneintrag;

1|0|2     Move 1 (86.0)
0|2|1     Move 3 (1.0)
1|2|1

Hier gibt es nur zwei legale Zugmöglichkeiten, die eine hat 85 mal zum Sieg geführt, die andere hat nie zu Sieg oder Niederlage geführt – kein Wunder, die führt immer zu unentschieden.

Die Frage, für welchen Zug man sich entscheiden soll, wenn mehrere nicht offensichtlich unsinnige zur Auswahl stehen, bleibt weiterhin erst einmal akademisch. Der Agent kann weniger oder mehr explorativ vorgehen, und entweder den jeweils bisher am höchsten bewerteten Zug wählen, oder auch einmal einem anderen eine Chance geben. Beim aktuellen Spiel macht das keinen Unterschied, aber das wird sich noch einmal ändern.

Das kleine Problem vom letzten Beispiel verschärft sich:

1|0|0     Move 1 (1.0)
0|0|0     Move 2 (1.0)
0|0|0     Move 3 (1.0)
          Move 4 (1.0)
          Move 5 (1.0)
          Move 6 (1.0)
          Move 7 (1.0)
          Move 8 (1.0)

Wenn Spielerin 1 ihr erstes Kreuz links oben macht, sind für den Agenten alle Zugmöglichkeiten von der gleichen Qualität. Keiner führt nämlich unmittelbar zu Sieg oder Niederlage, deshalb ändert sich die Bewertung nie, da mag der Agent so viel trainiert haben, wie er möchte. Aber erfahrene Spieler wissen: Fast alle Züge führen in dieser Situation zwar nicht automatisch, aber doch bei einer einigermaßen gewitzten Gegenspielerin im über-übernächsten Zug zu einer Niederlage, sind also ein Fehler. Nur Move 4 ist sinnvoll. Unser Agent hat bislang keine Chance, das zu lernen, weil der Q-Tabellen-Eintrag bislang immer nur vom unmittelbaren folgenden Feedback abhängt.

Hier eine Grafik, die das Problem noch einmal auf andere Weise darstellt. Die gelb markierten Züge sind die, die in der Situation zu einer gleich folgenden Niederlage geführt haben; die werden herabgestuft. Die orange markierten Züge sind die, die mittelbar zu einer Niederlage führen; ihr Wert bleibt nach dem bisherigen System leider unverändert:

Neu eingeführt in diesem Beispiel: Nichts, aber das Problem der Sackgassenzüge wird deutlicher.

Beispiel 5: Nim

Lasse ich weg, es gilt dafür das gleiche wie für Tic-Tac-Toe.

Beispiel 6: Breakout

In Breakout prallt ein Ball von allen Wänden und dem Schläger ab; der Agent soll lernen, den Schläger so zu steuern, dass der Ball erreicht wird. Berührt der Schläger den Ball, zählt das als Sieg; berührt der Ball den Boden, zählt das als Niederlage. Man lässt den Agenten eine Zeitlang spielen und alles ausprobieren und eine Q-Tabelle anlegen.

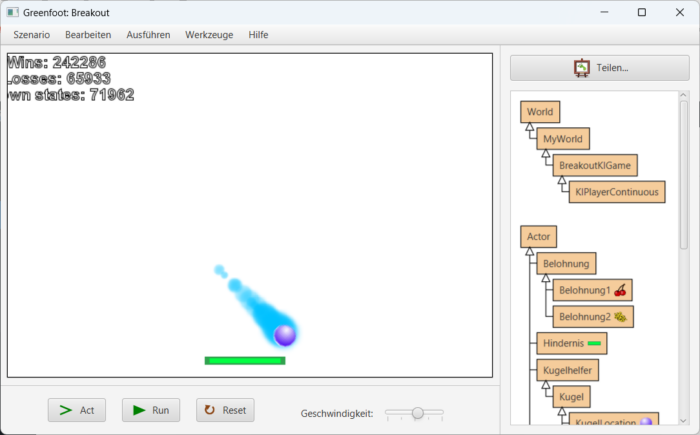
Die erste Frage, die man sich stellt: Welche Zustände sollen in die Q-Tabelle eingetragen werden? Relevant sind möglicherweise die x- und y-Position des Balls, die x-Position der Schlägers, die Geschwindigkeit des Balls (falls es da Unterschiede gibt) und sein Drehwinkel. Selbst wenn man großzügig rundet und das nicht pixelgenau misst, sonder gruppiert, landet man schnell bei 27000 Zuständen (experimentell herausgefunden bei den Dimensionen meines Spieles), die verwaltet werden wollen. Dazu aber mehr im nächsten Beitrag. Vorab: Wenn man schon weiß, welcher Faktor oder welche Faktoren wirklich relevant sind für die Lösung des Problem, kann man sich darauf beschränken. Und beim einfachen Breakout oben reicht die Differenz der x-Positionen von Kugel und Schläger. Alles andere ist vorerst egal. Dann gibt es je nach Spielfeldgröße und eventueller Pixel-Zusammenlegung nur ein paar Dutzend Zustände. – Die Anzahl der möglichen Entscheidung ist bei jedem Zustand ohnehin klein: Der Agent kann den Schläger nach links, nach rechts, oder gar nicht bewegen, abgekürzt L, R, N.

Die zweite Frage, die man sich stellt: Was soll als Sieg oder Niederlage gelten? Im nächsten Blogeintrag wird das differenzierter, aber für jetzt gilt einfach: Den Ball mit dem Schläger zu berühren zählt als Sieg, der Ball an der Unterkante des Spielfelds zählt als Niederlage.

Wird das reichen, um erfolgreich spielen zu lernen, oder werden wir wie bei Tic-Tac-Toe keinen Erfolg haben?

Nehmen wir an, wir haben den Zustand -12 oder +12. Der Schläger ist im einen Fall deutlich links vom Ball, im anderen weit rechts davon:

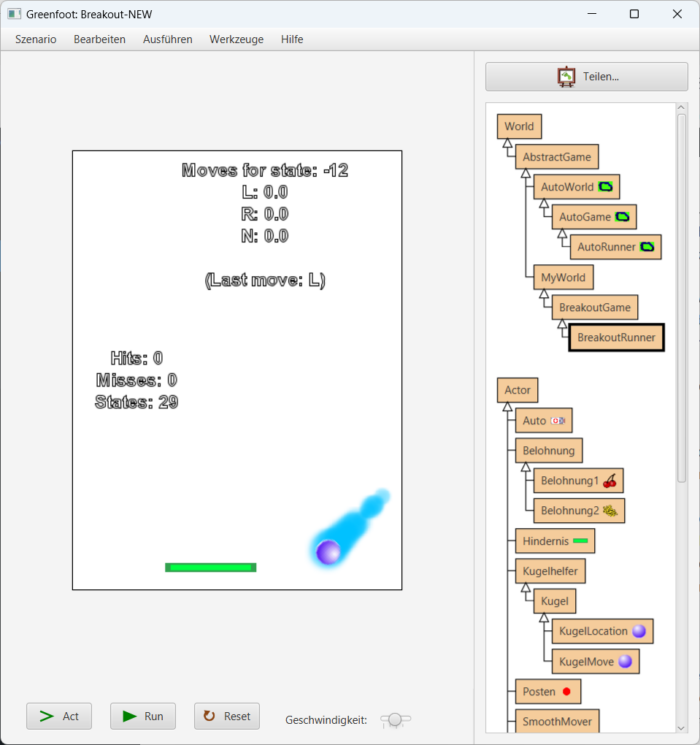
Wenn der Ball weit oben ist, wird sich die Q-Tabelle nicht ändern, weil unmittelbar weder Sieg noch Niederlage folgen. Wenn der Ball weit unten ist wie im Bild, führen weder L noch R noch N zu einem Erfolg, sondern alle zu einer Niederlage. Die Q-Werte werden demnach nach Durchführung der Bewegung herabgesetzt, aber im Mittel alle gleich viel. Es gibt mittelfristig keinen Favoriten. Zustand -12 oder +12 sagen dem System letztlich beide gar nichts.

Nehmen wir jetzt an, das Spiel ist im Zustand -7 oder +7 und gleichzeitig ist der Ball weit unten, so wie in diesem Bild:

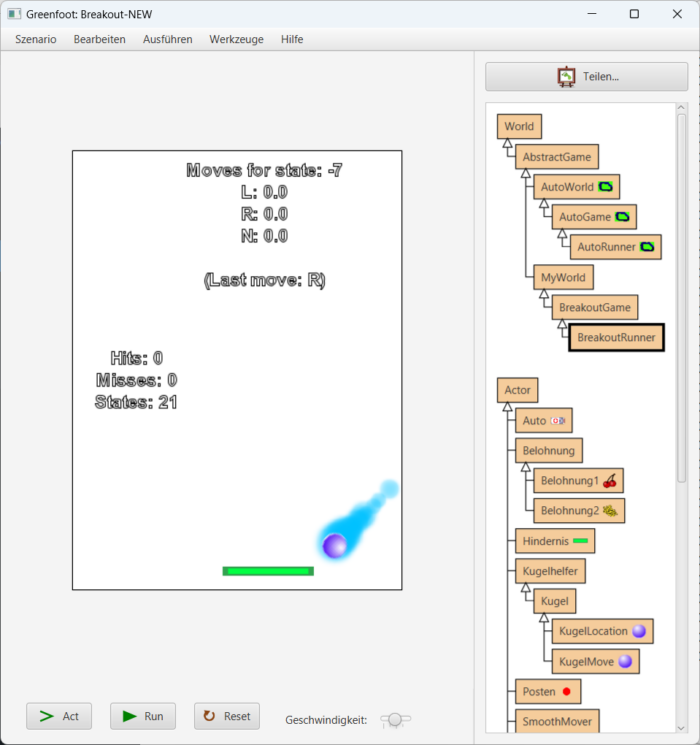
Dann ist der Schläger knapp links oder rechts vom Ball, und jetzt führt die eine Entscheidung zu Sieg und die andere nicht. Es wird also in diesem Zustand jeweils der Wert der entsprechenden Entscheidung heraufgesetzt. (Und die Zustände -6 bis +6 führen ohnehin nie zu einer Niederlage, und wenn der Ball weit unten ist, sogar zu einem Erfolg.)

Die KI kann also lernen, in einigen wenigen Grenzsituationen das richtige zu tun, in allen anderen Fällen wird sie zufällig agieren. Reicht das?

Ja, das reicht tatsächlich, um dieses simple Breakout spielen zu können. Hätte ich nicht gedacht! Warum klappt das da und bei Tic-Tac-Toe nicht? Bei Tic-Tac-Toe kommt der Agent nicht umhin, in einen blöden Zustand zu kommen, wo man schon verloren hat, es aber noch nicht weiß. Bei Breakout ist es so, dass der Agent früher oder später in einen aus einer kleinen Menge von erfolgreichen Zuständen kommt und sich immer nur innerhalb dieser Menge von Zuständen bewegt. Klarer wird das vielleicht im Video:

Dennoch, wenn das Spiel schwieriger wird, klappt das nicht mehr. Eine sinnvollere Methode zur Änderung der Werte in der Q-Tabelle, die auch bei Tic-Tac-Toe funktioniert, steht im nächsten Beitrag. (Fortsetzung folgt.)

Links:

• Roboterschach:
  https://computingeducation.de/proj-schlag-das-kroko/
  https://www.stefanseegerer.de/schlag-das-krokodil/
• Weiteres Material dort:
  https://computingeducation.de/proj-it2school/