(Fortsetzung von hier.)

Die Lösung des Problems, grundsätzlich

Das Problem vom letzten Mal war: Wenn man nur den Zug vor Sieg oder Niederlage bewertet, dann gibt es eben nur eine Lernmöglichkeit unmittelbar vor Sieg oder Niederlage und sonst nicht. Wenn man das Problem so formuliert, ist die Lösung einfach: Man bewertet nicht nur den letzten gemachten Zug, sondern jeden Zug, jedesmal. Es gilt dabei weiter: wenn ein Zug zu einer Niederlage führt, wird er herab-, wenn er zu einem Sieg führt, heraufgewertet. Neu ist: wenn ein Zug zu einer Situation führt, wo es nur schlechte Folgezüge gibt, dann wird er ebenfalls herabgewertet – hier ein Tic-Tac-Toe-Beispiel, Spieler 2 am Zug, alle Züge in dieser Situation führen zu einer Niederlage (so dass die KI lernen muss, diese Situation zu vermeiden):

1|2|0     Move 2 (-15.0)
2|0|0     Move 4 (-13.0)
1|0|1     Move 5 (-11.0)
          Move 7 (-15.0)

Und wenn andersherum ein Zug zu einer Situation führt, in der es mindestens einen sehr guten Zug gibt, dann wird die Bewertung des ersten Zugs heraufgesetzt.

Kurz: Bei jedem Durchgang wird der letzte Zug im vorhergehenden Zustand bewertet, und zwar abhängig von der Bewertung der Möglichkeiten im aktuellen Zustand (oder eben Sieg/Niederlage).

Reihenfolge:

1. Die KI befragt die Q-Tabelle nach der besten Entscheidung in der aktuellen Situation.
2. Diese Entscheidung wird durchgeführt; damit ändert sich die Situation.
3. Das Spiel meldet der KI Erfolg oder Misserfolg oder eine andee Bewertung der Situation zurück.
4. Die KI ändert den Eintrag in der Q-Tabelle für die alte, ursprüngliche Situation, und zwar in Abhängigkeit von der Bewertung des bestmöglichen Zugs in der jetzigen Situation. Wenn es in der neuen Situation einen tollen Zug gibt, wird der Wert der alten Zug-Situation-Kombination heraufgesetzt. Wenn es in der neuen Situation nur schlechte Züge gibt, wird der Wert der alten Zug-Situation-Kombination herabgesetzt.

Die konkrete Belohnungsfunktion, mit Lernrate und Diskontierung

Beim letzten Mal habe ich zwei Fragen vorgestellt, die man sich bei jedem solchen Spiel/Projekt stellt: Was wählt man als Zustand, und was zählt als Gewinn/Niederlage? Die vorläufigen Antworten waren: als Zustand nehmen wir bei Breakout die Differenz in der x-Position von Ball und Schläger, und Gewinn/Niederlage ist das Treffen oder Verfehlen des Balles mit dem Schläger. Wir bleiben vorerst bei diesen beiden Antworten, werden später aber etwas daran ändern müssen.

Bi der Funktion, mit der man den neuen Q-Wert für einen Zustand stateOld und einen Zug move berechnet, spielen neben dem aktuellen Zustand stateNew noch zwei Faktoren eine Rolle, deren Wert unterschiedlich eingestellt werden kann, der aber konstant bleibt: Diskontierungsfaktor/gamma und Lernrate/learning rate.

Diskontierungsfaktor/gamma: Kommt von discount/Nachlass/Ermäßigung/Skonto. Ist ein Wert zwischen 0 und 1 und bestimmt, wie sehr der höchstmögliche zukünftige Wert berücksichtigt werden soll. Vorschlagswert: 0.5

Lernrate: Ist ein Wert zwischen 0 und 1 und bestimmt, wie sehr der neue Wert (aus Erwartung und Belohnung zusammengesetzt) gegenüber dem alten dominiert. Vorschlagswert: 0.75

Dann sieht die Funktion so aus (reward ist die Belohnung/Bestrafung für Treffen/Ball im Aus/sonstwas):

public void update(String stateOld, String stateNew, double reward, int move)
{
  // (1) increase reward by (discounted) highest value in new state
  reward = reward + gamma * getHighestValue(stateNew);

  // (2) reduce reward by old value
  reward = reward - getValue(stateOld, move);

  // (3) apply learning rate to modified reward
  double change = reward * learningRate;

  // (4) increase value by calculated change
  increaseValue(stateOld, move, change);
}

Man kann es auch so sehen, dass der alte Wert erhöht wird um:
lernfaktor * (Belohnung + diskontierter Bestwert - alter Wert)

Meist sieht man die Formel für den neuen Wert so, was aber genau das gleiche ist:

neuerWertfür Entscheidung e in Zustand z = 
(1-lernrate) * alterWertfür Entscheidung e in Zustand z + 
lernrate * (belohnung + gamma * höchstwertfür eine Entscheidung in Zustand z+1

Wenn der Lernfaktor 0 ist, ändert sich gar nichts. Wenn der Lernfaktor 1 ist, wird der neue Wert ganz auf die Belohnung plus diskontierter Bestwert gesetzt, der alte Wert spielt keine Rolle dabei. Bei den Werten dazwischen gilt: Wenn die Summe aus Belohnung für den gemachten Zug und diskontiertem Bestwert im neuen Zustand größer ist als der alte Wert, dann erhöht sich dieser; wenn sie kleiner ist, verringt er sich.

Wenn der Discount-Faktor 0 ist, geht es einfach nur um die Belohnung, der Bestwert im neuen Zustand spielt keine Rolle. Wenn der Discount-Faktor 1 ist, spielt der Bestwert im neuen Zustand eine größere Rolle.

Die Formel kann man natürlich vereinfachen, dann geht das Berechnen vielleicht schneller. Sie reicht bereits, um etwa Nim oder Tic-Tac-Toe und natürlich auch Breakout spielen zu lernen (aber letzteres ging ja bereits halbwegs). Wenn es in Zustand 3 nur Züge gibt, die zur Niederlage führen, wird der Wert für die Entscheidung, die von Situation 2 zur Zustand 3 geführt hat, verringert. Und wenn es in Zustand 2 dann irgendwann einmal auch sonst nur niedrig bewertete Züge gibt, wird auch die Bewertung von einem Zug in Zustand 1, wenn er zu Zustand 2 führt, verringert. Sackgassen sprechen sich sozusagen nach und nach herum, und Strecken, die zum Ziel führen, ebenso. Wenn es viele Zustände gibt, dauert das aber sehr, sehr, sehr lange.

Funktioniert das?

Bei Breakout hat das ja schon im einfachen System geklappt, aber jetzt kann die KI eben auch Tic-Tac-Toe und Nim spielen lenen. Nur lässt sich das nicht so gut in einem Bild oder Film zeigen. Ich verspreche aber, dass diese neuen Bewertungen errechnet worden sind:

1|0|0     Move 1 (-0.0776515946578002)
0|0|0     Move 2 (-0.09491143167204687)
0|0|0     Move 3 (-0.08783116090423461)
          Move 4 (2.1469792068679446E-6)
          Move 5 (-0.09086642291797421)
          Move 6 (-0.1026154061878333)
          Move 7 (-0.09468690776157813)
          Move 8 (-0.09604017243001356)

Zug 4 hat keine sehr hohe Bewertung, aber die einzige nichtnegative. Es ist der einzige Zug, der auf diese Eröffnung hin bei einer versierten Spielerin 1 nicht zur späteren Niederlage von Agent 2 führt (aber vermutlich auch nicht oft zu einem Sieg, sondern eher zu unentschieden). Die ganz oben gezeigte Situation 120-200-101 wird also nach dem Training nicht mehr entstehen.

Neu eingeführt: Lernrate, Diskontierungsfaktor

Eine wichtige Entscheidung: Das Belohnungssystem

Das bisherige Belohnungssystem war sehr streng: Pluspunkte für Treffer, Minuspunkte für Aus, und sonst nichts. Ein anderes Belohnungssystem könnte darüber hinaus die Ergänzung haben: je größer die Entfernung Schläger-Kugel, desto größer fällt die negative Belohnung aus. Das motiviert, diese Entfernung gering zu halten. Damit ist der Agent noch viel schneller trainiert. Aber, finde ich, er ist dann nicht darauf trainiert, Breakout zu spielen, sondern darauf, den Schläger möglichst nah am Ball zu halten. Und das ist eine viel leichtere Aufgabe. Wenn man schon weiß, was die Lösung ist, kann man das Erlernen dieser Lösung beschleunigen.

Die zweite wichtige Entscheidung: Wie die Wahl der Zustände das Ergebnis beeinflusst

Bisher gab es bei Breakout nur ein paar Dutzend Zustände, die deswegen leicht zu verarbeiten waren; sie kamen immer wieder vor und hatten deshalb reichlich Gelegenheit, sich bei der Bewertung ihrer möglichen Züge zu wandeln und zu optimieren. Wenn es mehr Zuständ gibt, wird das schwieriger. Die Zustände hingen bisher ab von der Differenz in den x-Positionen von Schläger und Ball.

Ich finde das ein bisschen geschummelt. Wenn ich eh schon weiß, dass die Differenz in den x-Positionen wichtig ist und sonst nichts, dann habe ich der KI schon eine Menge Arbeit abgenommen. Wenn ich dagegen nichts vorgebe und als Zustand anbiete: die x-Positionen, aber auch die y-Position des Balls, und seine Flugrichtung noch dazu, dann habe ich, selbst bei grober Zusammenfassung (wo ich etwa nur 12 verschiedene mögliche y-Zustände für den Ball berücksichtige) immer noch knapp 14000 Zustände, und da dauert es lange, bis die sich oft genug wiederholt haben. Die KI findet dann zwar eine brauchbare Lösung, es dauert nur deutlich länger.

Die gefundene Lösung sieht dann aber auch anders aus, unsicherer, wackeliger: Beim einfachen Zustandssystem besteht sie darin, den Schläger immer parallel zum Ball zu führen, also die Differenz zwischen den x-Positionen klein zu halten. Beim komplexen Zustandssystem ist das wie im folgenden kurzen Film: Meistens ist es egal, wie der Schläger ein bisschen zappelt, aber wenn der Ball unten ist, wird der Schläger hektisch:

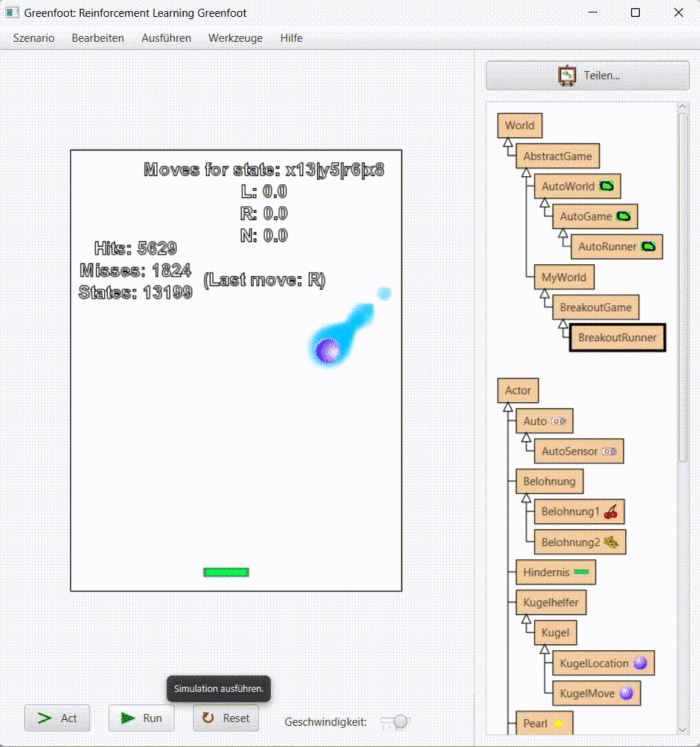
(Warum ändert sich oben nichts sondern alles bleibt bei 0? Weil der Startwert 0 ist, und wenn die Belohnung auch 0 ist, ändert sich selten etwas. Mit 1 als Startwert sieht man zwar ständige Veränderung, der Agent findet aber keine Lösung.)

Überblick über die ausprobierten Varianten

Ich habe verschiedene Kombinationen ausprobiert. Da ist einmal die Unterscheidung zwischen der einmaligen Rückmeldung vom letzten Blogeintrag (funktioniert nicht bei Tic-Tac-Toe, Nim, überhaupt allen schwierigeren Spielen) und der kontinuierlichen Rückmeldung aus diesem Beitrag. Zweitens kann ich die Berechnung der Belohnung streng halten oder bereits Wissen einfließen lassen. Drittens kann ich bei der Wahl der zustände bereits Wissen einfließen lassen oder nicht.

Für Breakout sieht der Unterschied beim Lernen so aus:

System der Rückmeldung	Berechnung der Belohnung via	Zustand:einfach (x-Differenz)	Zustand:schwierig (alle Daten)
Einmalig	x-Differenz (sehr leicht)	lernt schnell	spielt nach Lernphase nur rudimentär (außer bei großem Schläger)
Einmalig	Abstand zum Ball (leicht)	lernt schnell	spielt nach Lernphase allenfalls rudimentär (außer bei großem Schläger)
Einmalig	nur Sieg/Niederlage (schwer)	lernt schnell	spielt nach Lernphase allenfalls rudimentär (außer bei großem Schläger)
Kontinuierlich	x-Differenz (sehr leicht)	lernt schnell	lernt schnell
Kontinuierlich	Abstand zum Ball (leicht)	lernt schnell	lernt einigermaßen
Kontinuierlich	nur Sieg/Niederlage (schwer)	lernt schnell	lernt langsam, aber lernt

Und noch gar nicht herumgespielt habe ich mit unterschiedlichen Werten für Lernrate oder Diskontierung.

Eine kleinere Neuerung: Exploration

Das ist einfach! Normalerweise wählt der Agent in einem Zustand nicht einen zufälligen, sondern den qualitativ besten Zug, den mit dem höchsten Q-Wert laut Tabelle. Manchmal will man aber, dass der Agent abenteuerlustiger ist. Eine Explorationsrate von 0,05 besagt, dass in 5% aller Fälle stattdessen ein ganz zufällig ausgewählter Zug gewählt wird. Der Vorteil: Der Agent probiert auch mal etwas aus, das nicht erfolgsversprechend aussieht, und stößt so möglicherweise auf unerwartete Lösungen. Dieses explorative Verhalten kann man losgelöst von allen anderen Neuerungen betrachten.

int decideOnMove(String state) {
 if (Math.random()<explorationRate) { 
  return pickRandomMove(state);
 }
 else {
  return pickBestMove(state);
 }
}

Neu eingeführt: Die Explorationsrate.

Ausblick auf ein Problem

Wenn die Anzahl der Zustände zu hoch wird, stößt man mit einer Q-Tabelle an technische Grenzen. Schon die 14000 Zustände beim vereinfachten Breakout sind eigentlich zu viel. Vielleicht sind ja manche Elemente, die den aktuellen Spielzustand ausmachen, manchmal weniger relevant als andere und können je nach den anderen Elementen ignoriert werden? Dann benutzt man keine Q-Tabelle mehr, sondern ein Neuronales Netz – die Eingangswerte beschreiben den Zustand, die Ausgangswerte die möglichen Züge in diesem Zustand. Zu Erklärung und Beispiel werde ich aber wohl nicht mehr kommen, aber weiter unten sind ein paar Videos dazu verlinkt.

Ausblick: Alternativen zu Reinforcement Learning

Wenn ich die Lösung eh schon weiß, weiß ich brauche ich keine Q-Tabelle, insbesondere, wenn ich den besten Zug aus den gegebenen Variablen mit einer einfachen Formel berechnen kann. Bei dem Breakout-Spiel geht das zum Beispiel leicht, ich muss einfach schreiben: wenn x-Position von Schläger größer als x-Position der Kugel, dann gehe nach links, sonst nach rechts. Die Leistung der KI ist hier also nicht, auf eine Lösung zu kommen, die uns schwerer gefallen wäre.

Bei Tic-Tac-Toe ist das schon schwieriger. Auch da könnte ich mir vorher alle Züge selber überlegen und knackige Strategien formulieren. Außerdem es einfachere Algorithmen, dort auf eine Lösung zu kommen, etwa Minimax. Allerdings erfordert Minimax eine für jedes Spiel individuelle Bewertungsfunktion, das heißt, man muss sich als Mensch vorher mehr Gedanken gemacht haben, was eine gute Position und was eine schlechte ist – bei Maschinellem lernen findet das die KI selber heraus. Oder man macht das mit Brute Force durch Ausprobieren und Streichen von schlechten Zügen und rekursivem Streichen weiterer Zustände… aber sind wir damit nicht doch wieder bei unserer ganz einfachen Form von Reinforcement Learning?

Bei einem Spiel, wo ein Auto einen fixen Parcour entlang fahren soll, gibt es schnell viele Zustände und keine einfache oder offensichtliche Formel, was in welchem Zustand zu tun ist. Statt da mühsam von Hand zu überlegen, was in jedem Zustand das beste ist (links, rechts, geradeaus, bremsen, beschleunigen), lässt man den Agenten das einfach durch Ausprobieren und Belohnen lernen.

Fußnote: Unerwartetes Verhalten

Die KI versucht ihr Verhalten zu optimieren angesichts der Vorgaben bei der Programmierung. Manchmal passen diese Vorgaben aber nicht zum programmierten System und zeugen so Verhalten, das man so nicht gewollt hat. Von Beispielen hatte ich immer wieder gelesen, aber jetzt hatte ich selber solche Fälle. Hintergrund: Mein Breakout hatte ursprünglich einen Bug: Wenn der Schläger den Ball an einer bestimmten Position erwischte, irgendwo am Eck, dann rollte der Ball den Schläger entlang und prallte erst am anderen Ende des Schlägers wieder ab. Das war nur manchmal so und hatte bei meinem ursprünglichen Breakout-Projekt, in dem es noch gar nicht um Maschinelles Lernen ging, keine großen Auswirkungen, so dass ich mich nie darum gekümmert hatte, das mal zu beheben.

Die KI, mit dem Auftrag, Punkte zu machen, und das nämlich durch Berühren des Balls mit dem Schläger, hat den Bug und später eine Lücke im ersten Lösungsversuch gleich entdeckt und ausgenutzt.

Wie es weiter geht

Autorennen! Ich habe schon etwas zum Vorzeigen, ganz rudimentär, aber schon schick, scheitere aber noch an etwas, das gar nicht so viel mit dem KI-Element zu tun hat – das bleibt nämlich unverändert das bisherige. (Fortsetzung folgt also wahrscheinlich.)

Links:

• https://computingeducation.de/proj-snaip-A/
  mit sehr schönen Vorlage für Reinforcement Learning in Snap! – etwa: Pong, Breakout, Space Invaders
• https://www.youtube.com/watch?v=L4KBBAwF_bE
  ein Video zu einer KI, die Super Mario World gelernt hat (Q-Learning, aber nicht mit einer Q-Tabelle, sondern einem Neuronalen Netz).