1. Als eine Art Einleitung

Immerhin: Da steht schon einmal „Verben“, das war ein wörtliches Zitat aus einem Aufsatz. Ich kenne das auch in der allgemeineren Form: „Wörter wie ‚gleitet‘ und ‚vorüberrinnt’“ – und beides gehört zu meinen pet peeves bei der Deutschaufsatz-Analyse von Gedichten. Ich versuche, das meinen Schülern und Schülerinnen abzugewöhnen. Vielmehr soll man möglichst genau sagen: Was sind das für Wörter?

Ich erwarte in der Schule, wenn es um benotbare Aufsätze geht, einen recht analytischen Umgang mit Gedichten. Also nicht das, was ich oft bei Texten über Gedichte in der freien Wildbahn sehe oder in meiner alten Sammlung von Lyrikinterpretationen aus dem Referendariat. Da sind oft kluge Gedanken darin, aber die sind mitunter nur gestützt durch die Autorität des Autors oder der Autorin, oder stilles Einverständnis mit dem Publikum, so dass bestimmte Erkenntnisse vorausgesetzt werden. „Das Fest der Natur und der Seele wird Klang, jubelnd, leicht, tanzend und zugleich feierlich“ (Erich Trunz, Goethes Werke. Hamburger Ausgabe.) Im schulischen Aufsatzkontext darf und soll man das durchaus auch so schreiben, muss es aber davor oder danach erklären und begründen.

Ich möchte also zusätzlich zu: „Wörter wie ‚gleitet‘ und ‚vorrüberrinnt’“ eine Erklärung, was das für Wörter sind. Wörter ohne den Buchstaben a? Mehrsilbige Wörter? Das Gefühl, dass etwas diese Wörter verbindet, ist völlig legitim, und „Wörter wie“ legt immer den Eindruck nahe, dass es so eine Verbindung gibt. Aber zur benotbaren Analyse braucht es eine Erklärung des Zusammenhangs. „Verben“ ist einen Analyseschritt weiter als „Wörter“, „Verben der Bewegung“ noch weiter. Und vermutlich reicht das nicht, im Kopf ist da vielleicht schon eine bestimmte Art der Bewegung gemeint, und diesen Kopfinhalt zu versprachlichen, eventuell noch elegant, das ist dann die benotbare Analyse. Dass es noch andere Zugänge zu Lyrik und Literatur gibt: klar.

2. Der Anlass

All das ist die Einleitung zu einigen Gedanken zum neuen Lehrplan, hier für das Fach Informatik am Gymnasium. Solche Lehrpläne halten in Bayern zehn oder dreizehn oder auch mal fünfzehn Jahre. (Blogeintrag dazu.) Das heißt, dass ein neuer Lehrplan gar nicht so viele Jahre in Betrieb ist, bis schon wieder am neuen gearbeitet wird; und wer auch immer da entscheidet, hat schon vor fünf Jahren, vielleicht, entschieden, dass in Informatik 11 und 13 am Gymnasium Themen der Künstlichen Intelligenz drankommen. Das war vor GPT, aber nach AlphaGo und DeepL. Ich finde das sehr spannend, weil ich es noch nie erlebt habe, dass in so großem Umfang völlig neue Inhalte in einem Lehrplan auftauchen, die es bisher nie gab und die man auch nie im Studium gelernt hat. In Deutsch und Englisch gibt es ständig neue Bücher, aber das sind keine neuen Inhalte in diesem Sinn; man wendet bekannte Methoden darauf an. Neue Erkenntnisse in Erzähltheorie oder Phonologie: gibt es sicher, und fände ich sehr spannend; aber die tauchen in der Schule nicht auf. In Mathematik müssen die Lehrkräfte jetzt lernen, was Box-Plot-Diagramme sind, und in den Naturwissenschaften mit Tabellenkalkulation arbeiten; am Ende ist das für die auch so eine große Sache wie die KI-Einführung in der Informatik? Es erfüllt mich tatsächlich mit Freude, dass ich auf meine alten Tage noch einmal so viel Neues lernen kann/muss/darf.

Bayern legt sich jedenfalls ordentlich ins Zeug, die neuen Inhalte an die Lehrkräfte zu bringen. Es gab eine Online-Auftaktveranstaltung zur „Fortbildungsoffensive KI“ (der Name ein bisschen zu martialisch für meinen Geschmack), die einen Überblick gab. Da war noch nicht viel lernen, aber viel Information zu den eigentlichen Lernmöglichkeiten und vom Aufwand her eine Demonstration, wie hoch das Thema gehängt wird. Unterrichtsminister Piazolo war zugeschaltet, unverbindliche Worte zu Veränderungen durch KI, die Karotte einer möglichen Aufsatzkorrektur durch KI wurde vorgehängt. Die Expertin widersprach danach allerdings diskret; allerdings möglicherweise mit dem Fokus auf Benotung – nicht viele wissen, dass es auch unbenotete Korrekturen gibt, vielleicht, weil Deutsch das einzige Fach ist, in dem so etwas umfangreich vorgeschrieben ist.

Es gibt weiterhin 200 Seiten Handreichung (Link – vorläufig jedenfalls, die Ministeriumswebseite bietet keinen Permalink darauf an), die es nur als pdf gibt und nicht mehr auf Papier; einen Mebiskurs mit den Dateien dazu. Fußnote: Dieser Kurs ist inhaltlich in Ordnung, sehr ausführlich. Aber er ist furchtbar in der Usability. Er besteht lediglich aus Dateien in Verzeichnissen, die meisten gezippt. Und die alle herunterzuladen – was soll man auch sonst damit machen – ist enorm umständlich und ein elendigliches Hinundher-Gefrickel. Und die Videos habe ich verkleinert. 300 MB für 14 Minuten Screencast? Das ging dann auch mit 25 MB. – Es gibt Präsenzfortbildungen, für die man sich eintragen kann Es gibt einen Selbstlern-Moodlekurs an der ALP Dillingen, der als zehnstündige Fortbildung zählt und der tatsächlich nicht schlecht und ziemlich umfangreich ist. Ja, einige H5P-Elemente sind ein wenig überflüssig und haben etwas von „Wir müssen zeigen, was alles geht“, schaden aber auch nicht; aber ich habe dabei Neues gelernt und mir auf jeden Fall viele Anregungen geholt. Und um diese Anregungen soll es jetzt gehen.

3. Anregungen

Unter anderem wurde das Werkzeug „Demonstrator für maschinelles Lernen“ von Christoph Gräßl vorgestellt. Das deckt zwei Lehrplaninhalte von 11 ab, nämlich das Perzeptron (mein eigener Blogeintrag dazu) und den kNN-Algorithmus, k-nächster-Nachbar.

Der dient zu Folgendem: Wenn man eine Menge an bekannten Datensätzen hat, die bereits in zwei oder drei oder mehr Gruppen aufgeteilt sind („gelabelt“), entscheidet der kNN-Algorithmus, zu welcher dieser Gruppen ein neuer, bisher unbekannter Datensatz am ehesten gehört. Ob das in der Realität dann auch eine sinnvolle Zuordnung ist: andere Frage, man müsste separat überprüfen, ob kNN bei dieser Art Daten überhaupt anwendbar ist.

Der Algorithmus funktioniert letztlich so: Man schaut sich die k nächsten Nachbarn an. Zum Beispiel wählt man k=3. Das heißt, man schaut sich für den neu einzugruppierenden Datensatz die drei nächsten bekannten („gelabelten“) Datensätze an, und wenn die Mehrheit davon zu Gruppe A gehört, erklärt man den neuen Datensatz auch zu Gruppe A zugehörig.

Ein Beispiel, mit einem Screenshot aus dem Demonstrator:

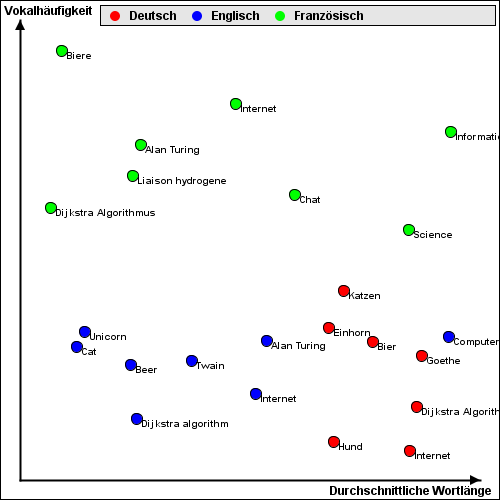
Die bereits bekannten, „gelabelten“ Datensätze sind als rote, grüne und blaue Punkte in einem Koordinatensystem eingetragen. Das Label ist jeweils Deutsch, Englisch oder Französisch. Jeder Datensatz besteht nur aus zwei Werten, zwei Dimensionen. Das ist praktisch und absichtlich, weil man das nur dann so schön in einem zweidimensionalen Koordinatensystem darstellen kann. Ursprung der Datensätze sind kurze Texte in englischer, französischer und deutscher Sprache; der Titel der Texte ist im Diagramm eingetragen. Der Datensatz selber enthält ja nur zwei Werte, nämlich durchschnittliche Wortlänge und durchschnittliche Vokalhäufigkeit. (Ich nehme an, damit sind die Buchstaben a, e, i, o, u gemeint; ob Umlaute dabei sind, weiß ich nicht; vokalisches y sicher nicht.)

Wenn man jetzt einen neuen Text eingibt, hier unten gelb markiert, schaut sich kNN mit k=3 die drei nächsten Nachbarn an:

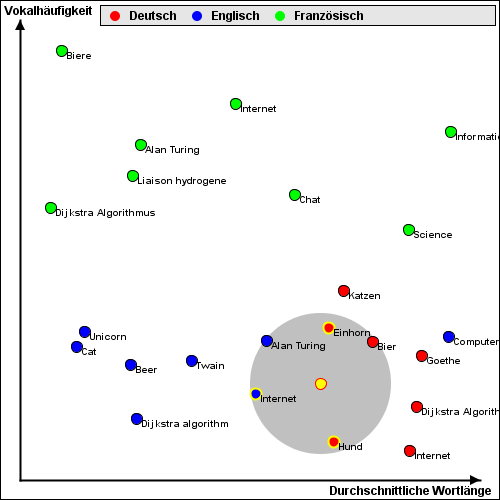
Hier ist die Nachbarschaft durch einen grauen Kreis markiert, die drei nächsten Nachbarn sind Einhorn (Deutsch), Hund (Deutsch) und Internet (Englisch). Die Mehrheit entscheidet, kNN weist dem neuen Text das Label „Deutsch“ zu, übrigens korrekt. Bei anderen Werten für k können andere Ergebnisse herauskommen.

Ein Knackpunkt dabei ist, was man unter Entfernung besteht. Der graue Kreis beruht nämlich auf dem euklidischen Abstand. Das ist der Abstand zweier Punkte, den man mit dem Geodreieck intuitiv messen würde, den man mit dem Satz des Pythagoras berechnen kann: Wurzel aus (x1-x2)² + (y1-y2)². Es gibt auch noch andere Möglichkeiten, die Entfernung zu berechnen, die lasse ich jetzt aber weg. Euklidisch ist praktisch, auch für später, und auch im dreidimensionalen Raum oder mit noch höheren Dimensionen.

4. Eigene Experimente

Man kann nicht nur einem gegeben Text zwei Werte zuweisen (durchschnittliche Wortlänge, durchschnittliche Vokalzahl), sondern zum Beispiel auch einem einzelnen Wort. Das könnte zum Beispiel Wortlänge und Vokalzahl sein. Oder… oder… die Wahrscheinlichkeit, in einem Text als erstes Wort in einem Satz aufzutauchen. Oder als letztes. Oder gerne nach „ich“. Oder… ach, da gibt es viele, viele Möglichkeiten.

Man muss sich das auch gar nicht selber überlegen. Es gibt bereits vorhandene Systeme, bei denen jedem Wort einer Sprache, oder zumindest einer großen Menge davon, Merkmalswerte zugewiesen sind; tatsächlich gilt das nicht nur für Einzelwörter, sondern auch für Wortgruppen, das ignorieren wir hier mal. Eine solche Bibliothek ist zum Beispiel fastText (Wikipedia). Man füttert fastText mit möglichst großen Mengen an Texten der Sprache, die einen interessiert, und gibt an, wie viele Werte („Dimensionen“) man gerne hätte, zum Beispiel 100. Und dann sucht sich fastText selbstständig 100 Dimensionen heraus und weist jedem Wort in jeder Dimension einen Wert zu. – Was eine Dimension jetzt tatsächlich bedeutet, ist nicht mehr auszumachen, eine allein bedeutet gar nichts, vielmehr werden Ähnlichkeiten zwischen Wörtern an parallelem Verhalten in diesem mehrdimensionalen Raum festgemacht.

Weil das viel Aufwand ist, gibt es für fastText bereits trainierte Modelle für knapp 300 Sprachen, man muss also nicht mehr selber so ein Modell erstellen sondern kann eines verwenden, das bereits jemand anderes vorbereitet hat. Wer sich auskennt oder einarbeitet, kann sich diese Modelle herunterladen und damit arbeiten. Bei mir ist weder das eine noch das andere der Fall, aber ich arbeite gerne mit der KI-Suite Orange (Blogeintrag), und die hat alles Nötige bereits integriert. Ein herunterladbares Muster ist auf den Orange-Seiten unter „Semantic Word Map“ zu finden. Es hat ein bisschen gedauert, bis ich das für meine Zwecke umgewandelt habe. Hinweise zur Erinnerung für später: (1) Wenn man das System kopiert und umbaut, man muss einmalig in der WordCloud alle Wörter auswählen. (2) Der Lemmatizer hat Probleme mit Umlauten; ausschalten.

(Der ganze Aufwand nur, um die Werte für die Wörter aus zwei Hofmannsthal-Gedichten zu kriegen. Das geht sicher auch einfacher, aber ich kann mir so auch noch andere Aspekte der Texte anzeigen lassen.)

Am Ende speichert man die Ergebnisse als Datei. Dann erhält man eine Tabelle mit den Wörtern, pro Wort eine Zeile. Mit den Einstellungen „fastText“ und „German“ bei DocumentEmbedding hat jede Zeile 300 Einträge für die 300 Dimensionen. Das sieht dann so aus (Ausschnitt):

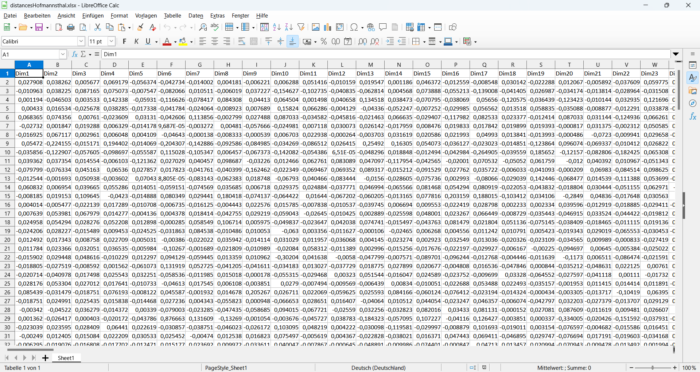
Was kann man jetzt damit machen?

Man kann zum Beispiel die Entfernung zwischen zwei Wörtern x und y berechnen. Das geht mit dem euklidischen Abstand, nur eben mit 300 statt mit 2 Dimensionen. Also (liest bei Wikipedia nach) nicht:

Wurzel( (x1-y1)2 + (x2-y2)2 ), 

sondern:

Wurzel((x1-y1)2+(x2-y2)2+(x3-y3)2+...+(x300-y300)2). 

Das wäre eine schlimme Formel, wenn man sie von Hand eingeben müsste, aber es gibt glücklicherweise eine Tabellenkalkulationsfunktion, die genau das macht: SUMMEXMY2(Zeile1; Zeile2) berechnet die Summe der Quadrate der jeweiligen Differenzen, wovon man nur noch die Wurzel nehmen muss, schon hat man die euklidische Distanz in diesem 300-dimensionalen Raum.

Zu abstrakt? Der errechnete euklidische Abstand zwischen „gleitet“ und „gleitet“ beträgt 0, das ist schon mal sinnvoll, die Wörter sind ja dieselben. Der Abstand zwischen „gleitet“ und „vorüberrinnt“ beträgt 0,71211 und der zwischen „gleitet“ und „Abend“ 1,14766; das erste Paar ist benachbarter. Welches Wort hat den größten Abstand zu „gleitet“? Untersucht man nur die Wörter dieses und eines weiteren Hofmansthal-Gedichts und ohne stop words, also Konjunktionen, Präpositionen, Pronomen und so weiter, kommt „Tod“ heraus, Abstand 2,22855. Der nächste Nachbar ist „gleitend“, dann „herüberglitt“, dann schon „vorrüberrinnt“, dann „unheimlich“. – Zur Erinnerung: Diese Werte kommen allein aus dem trainierten Datenmodell, haben also nichts mit den Hofmannsthal-Gedichten zu tun und wären für jeden anderen Text gleich. Ja, wenn ich fastText mit einem eigenen Hofmannsthal-Korpus anlernen würde… aber ich hör ja schon auf.

Die mit der Tabellenkalkulation erstellte Entfernungsmatrix:

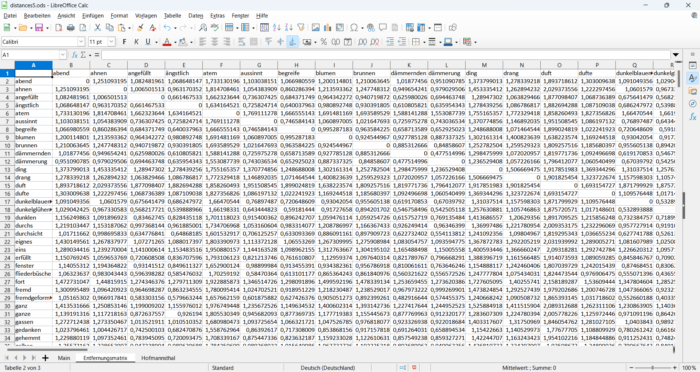
(Und ja, die kann mir auch schon Orange berechnen und ausgeben. Es kommen die gleichen Werte heraus, das beruhigt.)

5. Zurück zum kNN

Man könnte sich jetzt zehn Verben heraussuchen und als „Verb“ labeln und zehn Substantive und als „Substantive“ labeln. Und dann nimmt man ein neues Verb oder ein neues Substantiv und schaut, ob das mit kNN der richtigen Gruppe zugeordnet wird. Hier für „gleitet“ und die Entfernung zu je einigen willkürlich ausgewählten Verben und Substantiven:

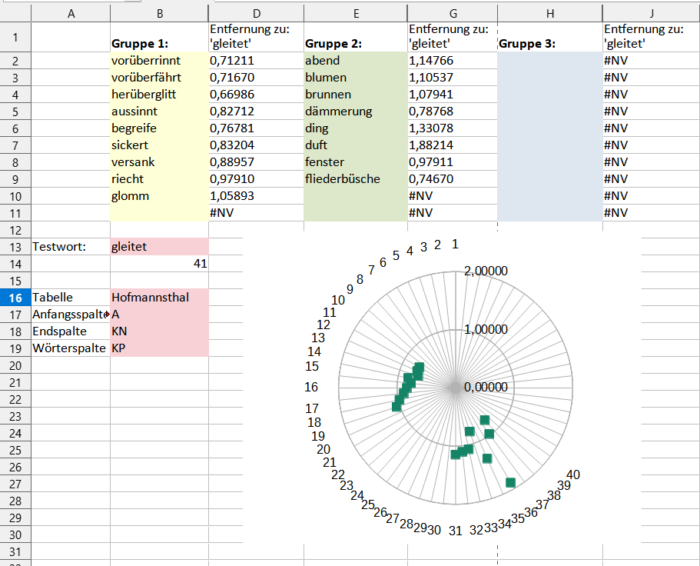
Stellt sich heraus, dass kNN für k=3 (aber auch für die anderen sinnvollen Werte) das Wort „gleitet“ eher in Gruppe 1 einordnet als in Gruppe 2. Also ist wohl syntaktische Funktion irgendwie enthalten in den 300 Dimensionen? Gegenproben zeigen aber, dass das nicht immer funktioniert, also vielleicht beruhen die relativen Ähnlichkeiten auf anderen Faktoren. Und auch sonst waren meine Ergebnisse gemischt; mit englischen Texten und knapp 400 Dimensionen aus einem anderen Modell habe ich bessere Erfahrungen gemacht, das aber nicht systematisch überprüft. Man müsste sich mal damit beschäftigen.

Das geht übrigens auch blockbasiert mit einer Art von Scratch, habe ich auch aus der Fortbildung: Unter https://playground.raise.mit.edu/main/ kann man links unten die Erweiterung „Text Classification“ ergänzen und erhält dann neue Blöcke, mit denen man ein Modell erstellen kann (also: Gruppen von Wörtern anlegen), um dann zu überprüfen, zu welcher Gruppe neue Wörter gehören. Das geht intern wohl auch über kNN, man sieht aber keine Details zum verwendeten Sprachmodell; es sollte aber wohl Englisch sein.

6. Zurück zur Ausgangsfrage

Hilft das alles irgendwie bei der Ausgangsfrage: Wörter wie „gleitet“ und „vorüberrinnt“? Nicht wirklich. Wenn ich ein solches Wort habe, kann ich mir die nächsten Nachbarn zeigen lassen; aber die Nachbarschaft kann auf allem möglichen beruhen. Wenn ich mehr Wörter habe, am besten deutlich mehr als nur zwei, kann ich für andere Wörter überprüfen, ob sie eher zu dieser Gruppe gehören als zu einer anderen, die ich dafür aber erst anlegen müsste. Das wäre dann sozusagen eine implizite Definition dessen, was man meint mit „Wörter wie“. Die eigentliche Leistung ist aber ohnehin, das passende Label für diese Gruppierung zu finden, und das nimmt einem zumindest dieses KI-System nicht ab.