Hintergrund

Ich habe meine Mathematik-Unterlagen aus der Kollegstufe eingescannt, Klasse 12 und 13, 1985 bis 1987. Andere Unterlagen als diese hatte ich nicht; für das schriftliche Abitur habe ich mich damit vorbereitet – und sehr wahrscheinlich, weil das so üblich war, mit einer zugekauften orangeroten Sammlung alter Abituraufgaben, obwohl ich mich nicht daran erinnern kann. Ich habe 15 Punkte im Abitur gekriegt.

Man kann den Scan herunterladen (PDF, 221 MB) und sich selbst ein Bild davon machen, wie damals Hefteinträge aussahen, oder meine Handschrift und Heftführung einer kritischen Würdigung unterziehen. Wer sich nur einen Überblick verschaffen möchte, für den habe ich hier alle erkennbaren Überschriften zusammengeschrieben: Den ersten, unbenannten Abschnitt (wohl: Analysis) und den darauf folgenden (Analytische Geometrie) verorte ich in K12, die anderen (Stochastik, Analysis, Analytische Geometrie) in K13.

Was mich überrascht hat

• Die strenge und strukturierte Nummerierung, für die sicher meine Lehrkräfte verantwortlich sind und nicht ich. Das Format geht dabei immer wieder mal durcheinander, das wiederum mag ich gewesen sein.
• Wie schmucklos und trocken all das ist. Mir hat es getaugt damals.
• Dass sich so wenig Kritzeleien, Kommentare, Fachfremdes an den Rändern finden. Ich war wohl diszipliniert, weil ich mich eigentlich als Kritzler eingeschätzt hätte. Insofern finden sich nur ein oder zwei kleine Sachen, nichts Spektakuläres, keine Mädchennamen und Herzen oder so.
• Dass einige nummerierte Punkte fehlen. Da war ich dann wohl nicht da. Hefteinträge nachträglich ergänzen, ich glaube, das war mir völlig fremd.
• Dass sich manche Elemente in K12 und K13 wiederholen. Spiralprinzip oder Lehrplanverwirrung, am Ende jedenfalls auch Wiederholung zur Abiturvorbereitung.
• Sollte ich meinen Deutschunterricht auch so aufziehen? Also, nummeriert, strukturiert, mit „Merke“ und „Definition“ und: 1. Der Satz, 1.1. Hauptssätze, 1.2 Nebensätze?

Nicht überrascht, weil ich das noch wusste, war ich von den Vektor-Variablen, die nur gelegentlich wie heute und international mit einem Kleinbuchstaben und einem Pfeil darüber dargestellt wurden (um sie von Skalaren zu unterscheiden), sondern fast durchgehend mit Sütterlin-Kleinbuchstaben, wie es bis dahin wohl noch üblich war.

Das Inhaltsverzeichnis

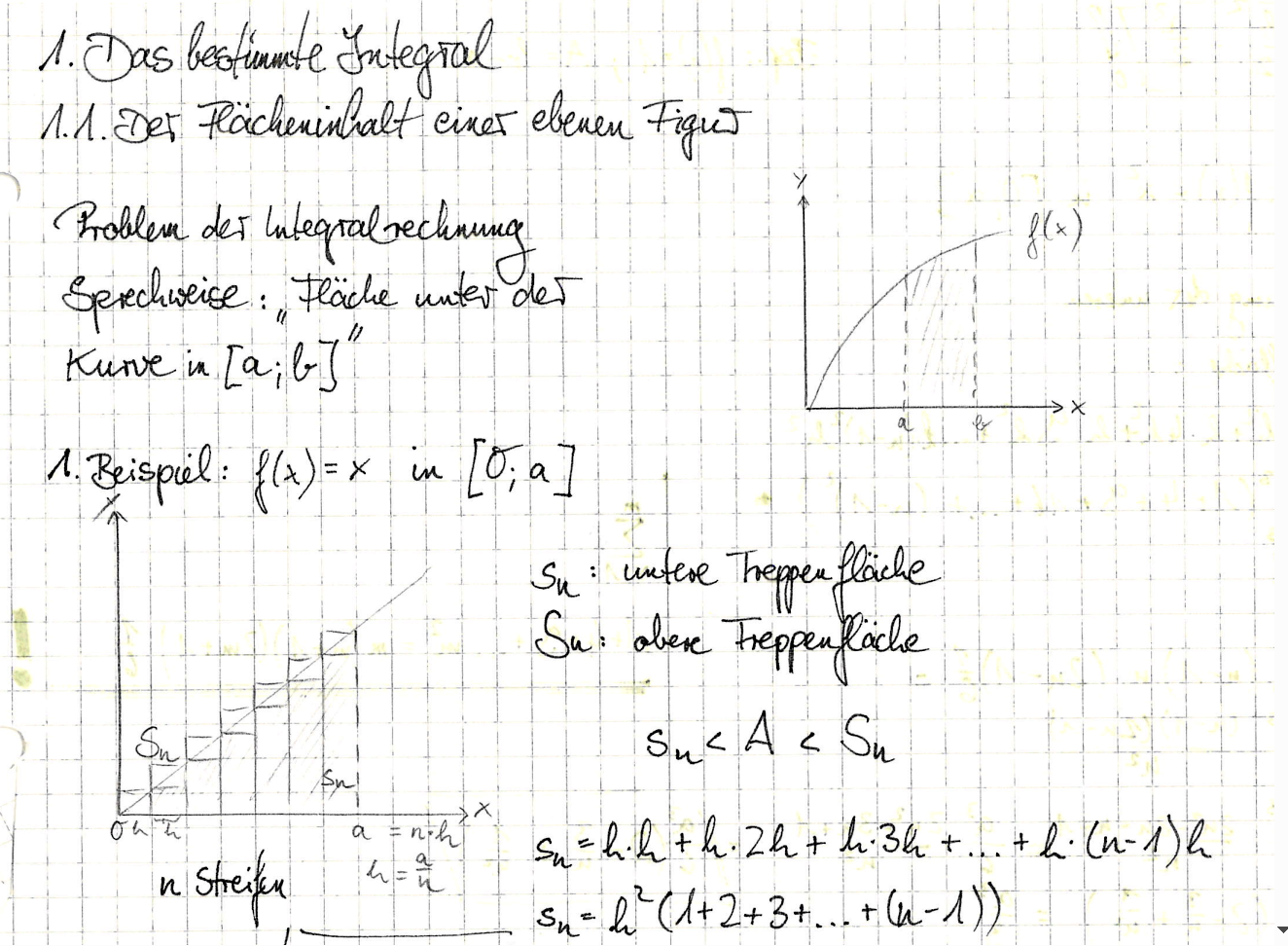
• 1. Das bestimmte Integral
  • 1.1 Der Flächeninhalt einer ebenen Figur
  • 1.2 Das bestimmte Integral
  • 1.4 Sätze über bestimmte Intergrale
  • Das Integral als Fkt. der oberen Grenze
  • Hauptsatz der Differential- und Integralrechnung
• 2.3 Anwendung des Hauptsatzes auf die Berechnung des bestimmten Integrals
• Kurze Wiederholung
• 2.4 Anwendung der Integralrechnung auf die Berechnung von Flächeninhalten
• 3. Die Ableitung der Umkehrfkt.
  • 3.1 Wiederholung der Umkehrfkt.
  • 3.2 Die Ableitung der Umkehrfkt.
• Logarithmusfunktion
• Logarithmus- und Exponentialfkt.
• 4.2 Identifizierung von L(x)
• 4.3 Grundformeln der Differntiation und Integration
• 4.4 Das logarithmische Differenzieren
• 4.5 Die Basis e als Grenzwert einer Zahlenfolge
• 4.6 Die natürliche Exponentialfkt.
• 4.7 Die allgemeine Exponentialfkt.

Analytische Geometrie

• I Vektorraum
  • 1. Geometrischer Vektorraum
    • 1.1 geometrische Definition von Vektoren
    • 1.2 Addition von Vektoren
    • Vektoren als Gruppe bez. der Addition
    • 1.3 S-Multiplikation von Vektoren
  • 2. Abstrakter Vektorraum
  • 3. Modelle
    • 3.3 Vektorraum der n-Tupel
• II Basis und Dimensionen
  • 1. Linearkombination
  • 2. Basis und Dimension
  • 3. Anwendung der linearen Unabhängigkeit bei geometrischen Beweisen und Aufgaben
• III. Koordinaten
  • 1. Basisdarstellung
  • 2. Das Rechnen mit Koordinaten
• V. Punktraum
• VI. Gerade und Ebene im R³
  • 1. Geradengleichung
    • 1.4 Sich schneidende und windschiefe Geraden
    • 1.5 Koordinatenform der Geradengleichung im R³
  • 2. Ebenen und Ebenengleichungen
  • 3. Zwei parallele Geraden
  • 2.4 Parallele und zusammenfallende Ebenen
  • 2.5 Sich schneidende Ebenen
  • 2.6 Schnitt von Gerade und Ebene
  • 2.7 Beispiel zum Schnitt von zwei Ebenen
  • Koordinatenform der Ebenengleichung
  • Darstellung der Ebene in Achsenabschnittsform
• VII. Teilverhältnis
• VIII. Das Skalarprodukt zweier Vektoren

I. Stochastik

• §1 Das Zufallsexperiment
• §2 Ergebnisraum Ω
  • 2.1 Def.
  • 2.2 Allgemeines Zufallsprinzip
• §3 Der Ereignisraum
  • 3.1 Def.
  • 3.2 Satz
  • 3.3 Relationen zwischen Ereignissen
  • 3.4 Definition
  • 3.5 Zusammenfassung
  • 3.6 De Morgansche Regeln
• §4 Relative Häufigkeit
  • 4.1 Definition
  • 4.2 Empirisches Gesetz der großen Zahlen
  • 4.3 Eigenschaften der relativen Häufigkeit
• §5 Der Wahrscheinlichkeitsraum
  • 5.1 Axiomensystem von Kolmogorow (1930)
  • 5.2 Bemerkung
  • 5.3 Wahrscheinlichkeitsverteilung
  • 5.4 Der klassische Wahrscheinlichkeitsraum (Laplace-Raum)
  • 5.5 Folgerungen aus dem Axiomensystem von Kolmogorow
• §6 Kombinatorik
  • Zusammenfassung [von Modellen]
  • 6.3 Der Binomialsatz
• §8 Die Bernoulli-Kette
  • 8.1 Das Bernoulli-Experiment
  • 8.2 Definition
  • 8.3 Definition
  • Bernoullische Formel
  • 8.6 Bernoullisches Urnenmodell
• §9 Testen
  • 9.1 Beispiel zum Signifikanztest
  • 9.2 Variante des Signifikanztestes
  • 9.3 Spezialfall des Signifikanztests

Analysis

• §1 Differentiationsregeln
  • Summenregel
  • Produktregel
  • Kettenregel
  • Quotientenregel
• §2 e- und ln-Funktion
• §3 Rationale Funktionen
  • 3.2 Verhalten im Unendlichen
  • 3.3 Polynomdivision
  • 3.4 Kurvendiskussion
• §4 Integration
  • 4.2 Integrationsregeln

Analytische Geometrie

• §0 Wiederholung
  • 0.1 Lage zweier Geraden
  • 0.2 Lage zweier Ebenen
  • 0.3 Das Skalarprodukt im R³
• §1 Die Normalform der Geraden
  • 1.1 Satz
  • 1.2 Satz
  • 1.3 Orientierung der Normalenform
  • 1.4 Definition
• §2 Die Normalenform der Ebene im R³
  • 2.1 Satz
  • 2.2 Satz
  • 2.3 Orientierung
  • 2.4 Def.
  • 2.5 Definition
  • 2.6 Lage des Punktes P
• 4. Abstände
  • Punkt – Punkt
  • Punkt – Ebene
  • Gerade – Ebene
  • Ebene – Ebene
  • Punkt – Gerade
• §3 Musteraufgaben
  • 3.1 Die Winkelhalbierenden von Geraden (Ebenen)
  • 3.2 Spiegelung
• Orthogonale Projektion
  • Punkt auf Ebene
  • Gerade auf Ebene
  • Punkt auf Gerade

Der Scan

Scan herunterladen (PDF, 221 MB).