Es gibt eine Art Computerspiel namens Life, nach dem Erfinder auch Conway’s Game of Life genannt. Man spielt nicht selber mit, sondern man setzt ein paar Zellen in eine leere Welt und schaut zu, wie sie sich vermehren oder sterben. Das sieht zum Beispiel so aus:
Die Regeln für das Überleben, Fortpflanzen und Sterben lauten so:
- Fortplanzung: Hat eine unbesetzte Zelle genau drei lebende Nachbarn (in den acht umgebenden Feldern), dann entsteht in der nächsten Generation dort eine neue lebende Zelle.
- Leben oder Tod: Eine lebende Zelle mit genau 2 oder 3 Nachbarn überlebt in die nächste Generation. Bei mehr oder weniger Nachbarn stirbt sie.
Wenn man das ein paar Mal mit verschiedenen Ausgangskonstellationen spielt, stellt man einige Sachen fest. Es gibt zum Beispiel manche Kombinationen aus Zellen, die stabil sind: der Brotkorb oder die Bienenwabe etwa. Wenn die nicht gestört werden, dann stirbt keine Zelle und keine neue entsteht.
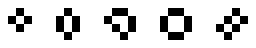
(Arbol1, CC-BY-SA, Quelle)
Dann gibt es noch Kombinationen, die oszillierend stabil sind. Am einfachsten ist der Blinker, der periodisch zwischen zwei verschiedenen Formen wechselt.
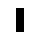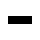
(Arbol1, CC-BY-SA, Quelle)
Und dann gibt es noch die Gleiter. Die sehen so aus, als bewegen sie sich fort, und zwar diagonal. Immer nach vier Takten haben sie sich horizontal und vertikal eine Zelle weiterbewegt.

(Quelle)
Insgesamt stellt man bei den ersten Versuchen fest, dass früher oder später die Welt zur Ruhe kommt und nur noch aus stabilen Figuren besteht und vielleicht einigen Gleitern dazu, die immer weiter in die Unendlichkeit hinausfliegen: Die Gesamtpopulation wächst nicht mehr.
Bald nachdem Conway das kleine Spielchen erfand, stellte er eine Herausforderung: Kann es eine Startpopulation von Zellen geben, die immer größer wird? Fünzig Dollar schrieb er aus und rechnete laut Wikipedia nicht damit, sie zahlen zu müssen.
Bis dieses Ding erfunden würde: eine Gleiterkanone.

(Quelle)
So sieht sie in Betrieb aus:
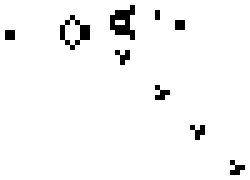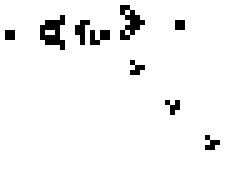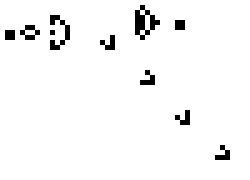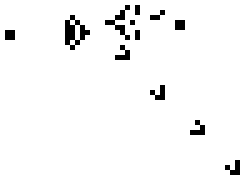
(Kieff, CC-BY-SA, Quelle)
Periodisch entsteht ein neuer Gleiter, und damit war gezeigt, dass die Gesamtpopulation bei Life immer weiter ansteigen kann.
Das war aber nur der Anfang. Weitere Gleiterkanonen wurden entdeckt. Bald kamen die Raumschiffe dazu: LWSS, MWSS, HWSS (lightweight/middleweight/heavyweight spaceship) und kompliziertere Varianten.
Nach und nach entstanden immer umfangreichere Populationen. Es gibt „Puffer“, das sind Konvois von Zellen, die sich zum Beispiel nach rechts bewegen und dabei einen Strom von Müll hinterlassen – Müll, der sich nach kurzer Zeit zu Gleiterkanonen entwickeln kann, die dann das tun, was sie am besten können – Gleiter produzieren. Es gibt „Filler“, die versuchen, die Welt mit so vielen Zellen und so rasch wie möglich zu füllen. Man geht davon aus, dass die maximale Zellendichte 50% beträgt.
Und dann wurde es noch komplizierter. Primzahlberechnung: Eine Population, die einen Strom von Gleitern erzeugt, und nur jeden x-ten Gleiter durch ein Tor passieren lässt – und zwar dann, wenn x eine Primzahl ist. Nachbildungen verschiedener elektrischer Schaltkreise, mit einem kontinuierlichen Strahl von Gleitern als informationstragendem Stromfluss. Und wenn man Schaltkreise hat, dann kann man auch einen Computer nachbauen, wenn man denn wollte. Ja, mit Life kann man alles berechnen, was man berechnen kann. Die folgende Population berechnet Fermat-Primzahlen:

Eine Fermat-Zahl hat die Form Fn = 2(2n) + 1, wobei n eine natürliche Zahl ist. Für n = 1 bis 5 sind die entstandenen Zahlen Primzahlen, vermutlich gibt es keine weitere Fermat-Zahl, die prim ist. Die Life-Konfiguration oben wird rechnen und rechnen, und wenn noch eine Fermat-Zahl herauskommt, wird sie sich auflösen.
Vom Berechnen:
Stellen wir uns diese zugegebenermaßen arg unwahrscheinliche Situation vor: Ein Lehrer gibt seinen Schülern den Auftrag, jeweils ein eigenes Life-Muster zu erzeugen, für ein Poster vielleicht. Er möchte, dass jeder ein eigenes entwirft, und nicht einfach das von einem Mitschüler nimmt und lediglich ein paar Generationen weiterlaufen lässt. Weil der Lehrer viele Schüler hat, hätte er gerne ein Computerprogramm, in das man zwei beliebige verschiedene Momentaufnahmen einer Life-Welt eingibt, und das Programm rechnet aus, ob es möglich ist, dass sich die eine Situation aus der anderen entwickeln kann oder nicht. Wenn das Programm ausspuckt: Jawoll, dieser eine Zustand kann sich nicht aus dem anderen entwickeln, die sind grundverschieden, dann weiß der Lehrer, dass hier zumindest kein einfaches Abschreiben stattgefunden hat.
Nur ist es leider unmöglich, so ein Programm zu schreiben. Braucht man gar nicht erst versuchen. Wird nicht gehen. Nie nicht. Das ist so quasi das Perpetuum Mobile der Informatik: Kann nicht sein.
Denn das Problem ist unentscheidbar. Das ist ein Fachbegriff aus der theoretischen Informatik, den ich bei den formalen Sprachen immer mal wieder erwähnt habe. Die genaue Erklärung muss warten, bis ich meinen Eintrag zu Chomsky 0 schreibe, der Menge der Sprachen, die immerhin semi-entscheidbar sind. Grundsätzlich kann man kein Programm schreiben, das überprüft, ob zwei andere Programme sich unter allen Umständen und für alle Eingabewerte immer gleich verhalten werden. Ein „Programm“ ist dabei alles, was so viel berechnen kann wie eine Turingmaschine, oder eine simple Programmiersprache, die einigen wenigen Kriterien genügt. (Oder was man mit dem Lambda-Kalkül beschreiben kann. Aber da begebe ich mich endgültig auf halbverstandenes Terrain.)
Und ja, jemand hat auch eine Turing-Maschine mit Life produziert:
Fußnote: Genau genommen ist Life ein Beispiel für einen Zellautomaten. Die bestehen aus vielen benachbarten Zellen (im diesem Fall in einer Schachbrettwelt, es könnte aber auch eine Welt aus Sechseckfeldern oder eine dreidimensionale sein), die bestimmte Zustände annehmen können (in diesem Fall nur zwei, lebendig oder unbelebt, es könnten aber auch mehr sein) und die nach bestimmten Regeln ihre Zustände ändern.
Links:
- Golly (schöne Life-Implementierung für verschiedene Plattformen; mitgeliefert vieleviele Beispiele)
- Wikipedia-Eintrag (deutsch) und Wikipedia-Eintrag (englisch) – beide sind lesenswert
- andere Vermehrungs-/Todes-Regeln für die Life-Welt und was dabei passieren kann (Wikipedia)
Schreibe einen Kommentar