Wie es angefangen hat, weiß ich nicht mehr. Irgendwann in der Mitte wollte ich jedenfalls wissen, wie das mit dem automatischen Erkennen von Musikstücken geht – man spielt zehn oder zwanzig Sekunden eines Liedes vor, und das Handy meldet sich danach und sagt einem, von wem das Lied ist und wie es heißt.
Beim Googeln stieß ich auf diese phantastische Seite darüber, wie einer genau das in Java nachbaute. Einfach, nachvollziehbar, übersichtlich. Allerdings ist der Code nicht vollständig, das hängt auch mit Drohungen des Marktführers zusammen, das gegen Patente verstoßen werde. Nicht glaubwürdig, aber ich verstehe sehr gut, dass man da als kleiner Blogger vorsichtig ist.
Trotzdem habe ich den Code nach und nach vervollständigt und nachprogrammiert und dabei viel gelernt.
Schritt 1: Mikrofon anschließen und mit Java Ton vom Mikro aufnehmen
Funktioniert. Wie so eine Aufnahme aussieht, das kennt man aus dem Fernsehen:

Allerdings, wenn man mit der Lupe richtig nahe herangeht, sieht man, dass die Wellen, die man zu sehen meint, gar keine sind: Stattdessen sind einfach nur eine Menge von Punkten gespeichert, die in gleichmäßigem Abstand einer nach dem anderen eingezeichnet werden.

Das passiert nämlich beim Digitalisieren von Schallwellen. Es wird nämlich gar keine Schallwelle gespeichert, sondern in regelmäßigen Abständen gemessen, was gerade an Schall hereinkommt. Regelmäßige Abstände heißt: häufig misst man 44100 mal pro Sekunde. (Damit erwischt man Frequenzen von bis zu 22050 Hz.) Wie viel verschiedene Amplituden (also Lautstärken, die vertikale Position des eingetragenen Messpunkts) möglich sind, hängt von einem weiteren Wert ab. Reserviert man pro gespeichertem Punkt 1 Byte (8 bit), dann kann man zwischen 256 verschiedenen horizontalen Positionen wählen. Bei 2 Byte (16 bit) sind es schon 65536. Und wenn man richtig genau sein woll, nimmt man 4 Byte (32 bit) pro Punkt. Der Einfachkeit halber habe ich mit 8 bit pro Punkt gearbeitet, was sicher keine high-fidelity Aufnahme ermöglicht.
Gespeichert wird die Aufnahme also in einer langen Reihe von Bytes. Wenn man die Bytes als ganze Zahlen interpretiert, sieht ein Ausschnitt etwa so aus:
-50, -45, -37, -31, -26, -24, -25, -26, -26, -28, -26, -25, -22, -18, -11, -4, 5, 13, 20, 24, 29, 31, 33, 34, 32, 29, 23, 16, 7, 1, -4, -6, -8, -7, -8, -6, -5, -3, 1, 7, 12, 16, 16, 9, 0, -10, -20, -22, -19, -12, -1, 9, 16, 21, 22, 22, 21, 21, 19, 20, 19, 18, 18, 19, 20, 22, 22, 23, 20, 18, 14, 10, 3, -4, -11, -21, -31, -39, -49, -54, -59, -59, -59, -57, -51, -44, -32, -20, -5, 7, 18, 23, 22, 20, 15, 13, 13, 16, 24, 30, 36, 39, 41, 42, 43, 44, 45, 46, 45, 43, 39, 35, 29, 24, 17, 12, 4, -1, -7, -13, -19, -25, -32, -37, -43, -50, -55, -61, -64, -69, -71, -75, -74, -74, -69, -63, -55, -47, -42, -42, -43, -48, -52, -54, -52, -45, -37, -24, -14, -3, 5, 15, 21, 30, 35, 38, 40, 38, 33, 27, 19, 13, 4, -3, -11, -16, -22, -25, -30, -32, -35, -36, -38, -39, -40, -42, -46, -49, -55, -59, -63, -64, -63, -56, -48, -37, -26, -20, -14, -13, -12, -10, -8, -1, 5, 12, 17, 19, 21, 20, 22, 22, 24, 23, 23, 20, 20, 18, 18, 19, 19, 20, 19, 18, 16, 15, 12, 12, 10, 12, 15, 19, 24, 31, 36, 44, 48, 55, 60, 68, 75, 84, 91, 99, 101, 99, 94, 84, 76, 66, 61, 56, 50, 44, 34, 24, 11, 1, -10, -16, -24, -28, -32, -35, -36, -33, -30, -26, -22, -20, -17, -17, -14, -12, -9, -8, -5, -3, 0, 4, 11, 18, 28, 36, 42, 46, 49, 52, 57, 61, 66, 67, 68, 63, 58, 50, 46, 43, 43, 47, 49, 50, 46, 42, 36, 28, 23, 15, 7, -3, -16, -25, -34, -40, -41, -43, -44, -48, -55, -60, -65, -71, -74, -79, -84, -89, -94, -98
(Das sind 318 Punkte. Bei 44100 Punkten pro Sekunde macht das gut 0,007 Sekunden, bei 32000 Punkten pro Sekunde sind das knap 0,01 Sekunden.)
Wenn ich diese Zahlen in mein Tabellenkalkulationsprogramm eintrage und mir als Diagramm anzeigen lasse, sieht man, dass das tatsächlich irgendwie den im Audioprogramm dargestellten Werten entspricht:
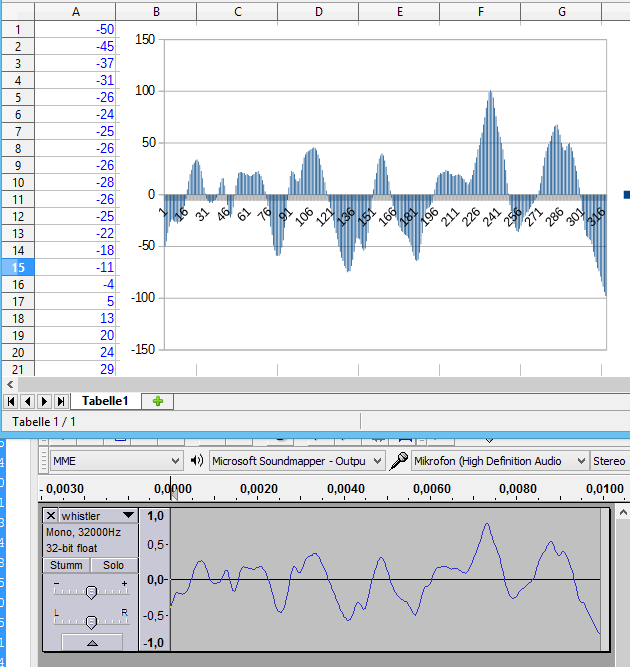
(Tatsächlich exportiert mein Audioprogramm das 8-bit-Wav-Format nur als „unsigned“, das heißt ohne Vorzeichen, also zu lesen als Zahlen von 0 bis 255. Für Java musste ich das umrechnen, da Java grundsätzlich mit „signed“ Bytes arbeitet, die als Zahlen von -128 bis 127 zu lesen sind.)
Schritt 2: Umwandeln der gemessenen Zahlenwerte in Frequenzen
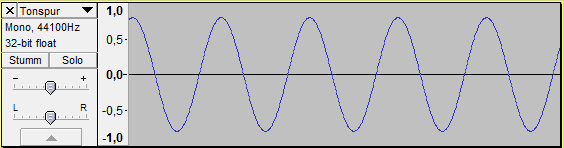
Man kann die Audioaufnahme beschreiben – und speichern – als einen Haufen Messpunkte, kontinuierlich aufeinanderfolgend in regelmäßigen Zeitabständen, so wie oben. Für manche Dinge ist diese Betrachtungsweise aber nicht so praktisch. Die folgende Aufnahme könnte man – statt auf Messpunkte zurückzugreifen – eleganter beschreiben als eine regelmäßige Schwingung.
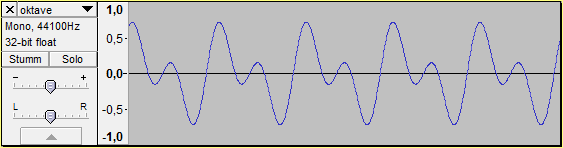
Und die folgende Aneinanderreihung von Messpunkten kann man prägnant unter einem anderen Gesichtspunkt beschreiben als: eine regelmäßige Schwingung und gleichzeitig eine von doppelter so großer Frequenz. (Ein Ton und die Oktave darüber.)
Tatsächlich kann man jede beliebige Sammlung von Punkten als eine Überlagerung von Wellen darstellen. Selbst die komplizierte Sammlung von oben:

Tatsächlich lassen sich diese 318 Messpunkte auch darstellen als eine Überlagerung von (höchstens) 318 verschiedenen Schwingungen. Die Umwandlung von n Messpunkten in n Schwingungen, mit relativen Frequenzen von 1 bis n heißt Fourier-Transformation, und davon hört man gelegentlich Mathelehrer Anekdoten aus dem Studium erzählen.
Und weil ich wissen wollte, was es mit dieser Fourier-Transformation auf sich hat, bin ich auf diese Seite gestoßen: An Interactive Guide To The Fourier Transform.
Genial erklärt, jedenfalls für einen Laien wie mich. Hilfreich sind auch zwei hervorragende Werkzeuge zum Verständnis, eines erst im Anhang. Bei dem ersten kann man einfach eine Reihe von Messpunkten eingeben, egal welche, und das Programm spuckt die entsprechenden Schwingungen aus. (Und umgekehrt auch.) Die drei Punkte 1, 0, 2 trifft man mit der Kombinationen aus folgenden Wellen:
Quellcode, basierend hierauf. MIT License. Blogeintrag dazu.
Um wirklich schön damit zu spielen, muss man den verlinkten Beitrag lesen.
Beim anderen Programm sieht man gut, was Kreise und Schwingungen und überlagerte Schwingungen miteinander zu tun haben.
Außerdem habe ich mir auf der Seite gleich noch den Sinus erklären lassen und die Eulersche Zahl. Erhellend!
3. Wie es bei dem ursprünglichen Projekt weiter geht
Die gespeicherten Bytes (die Messpunkte) werden umgewandelt in Schwingungen. Das geht so: Man nimmt einen Packen Bytes, zum Beispiel 2048. Diesen Packen wandelt man um in 2048 Schwingungen, eine mit Frequenz 1, eine mit Frequenz 2, eine mit Frequenz 3 und so weiter. Zu jeder Frequenz gehört eine Amplitude (wie laut, also die vertikale Komponente) und die Phase. Wenn man den verlinkten Blogeintrag gelesen hat, ist das kein Problem mit der Phase – das ist die Verschiebung der Welle nach rechts oder links, was wichtig dafür ist, welche Wellen sich mit welchen anderen aufheben oder hochschaukeln. Jede Schwingung wird gespeichert als komplexe Zahl (auch die kann man sich schön erklären lassen). Wo also vorher 2048 Bytes da waren, sind jetzt 2048 komplexe Zahlen, jede für eine eigene Frequenz.
Auf Basis dieser 2048 Frequenzen, jeweils mit mehr oder weniger großer Amplitude, wird dann quasi ein Fingerabdruck der Aufnahme gemacht, der dann später mit einer gespeicherten Kartei solcher Fingerabdrücke verglichen wird. Wie das geht: anderes Thema.
Schreibe einen Kommentar