Schlagwort: Programmierprojekte
-

Greenfoot Reinforcement Learning: jetzt über Git verfügbar
(8 Kommentare.) Ich habe jetzt endlich mein Greenfoot-Reinforcement-Material (siehe alter Blogeintrag, und die davor) aufgeräumt, vereinfacht und dokumentiert. Das habe ich zwar schon vor ein Tagen verkündet, aber jetzt gilt es wirklich. Und zwar ich habe das ganze Projekt nach Github Codeberg verlegt: https://codeberg.org/HerrRau/GreenfootReinforcementLearning/#readme Dort kann ich meine Verbesserungen aktuell halten und die Anleitung ständig…
-

Ferienaufräumen: App in Google Play Store gestellt
(13 Kommentare.) Ferienzeit ist bei mir Aufräumzeit. Und deswegen habe ich jetzt endlich die App, über die schon mal geschrieben habe (Juli 2023, August 2023) so weit fertiggestellt, dass ich sie in den Play Store stellen konnte. Ich komme ja nur in den Ferien zu so etwas und freue mich stets sehr darüber, dass mein…
-
Erfahrungen beim Spieleentwickeln
(5 Kommentare.) Gut, ich konnte die Finger doch nicht vom Programmieren lassen. Also bin ich weiter an dieser Idee geblieben. Stand: (Man kann immer noch zu zweit oder dritt oder viert spielen.) Ich finde es interessant, welche Gedanken ich mir so beim Entwickeln mache. Dass ich dabei nicht nach einem System vorgehe oder wie jemand…
-
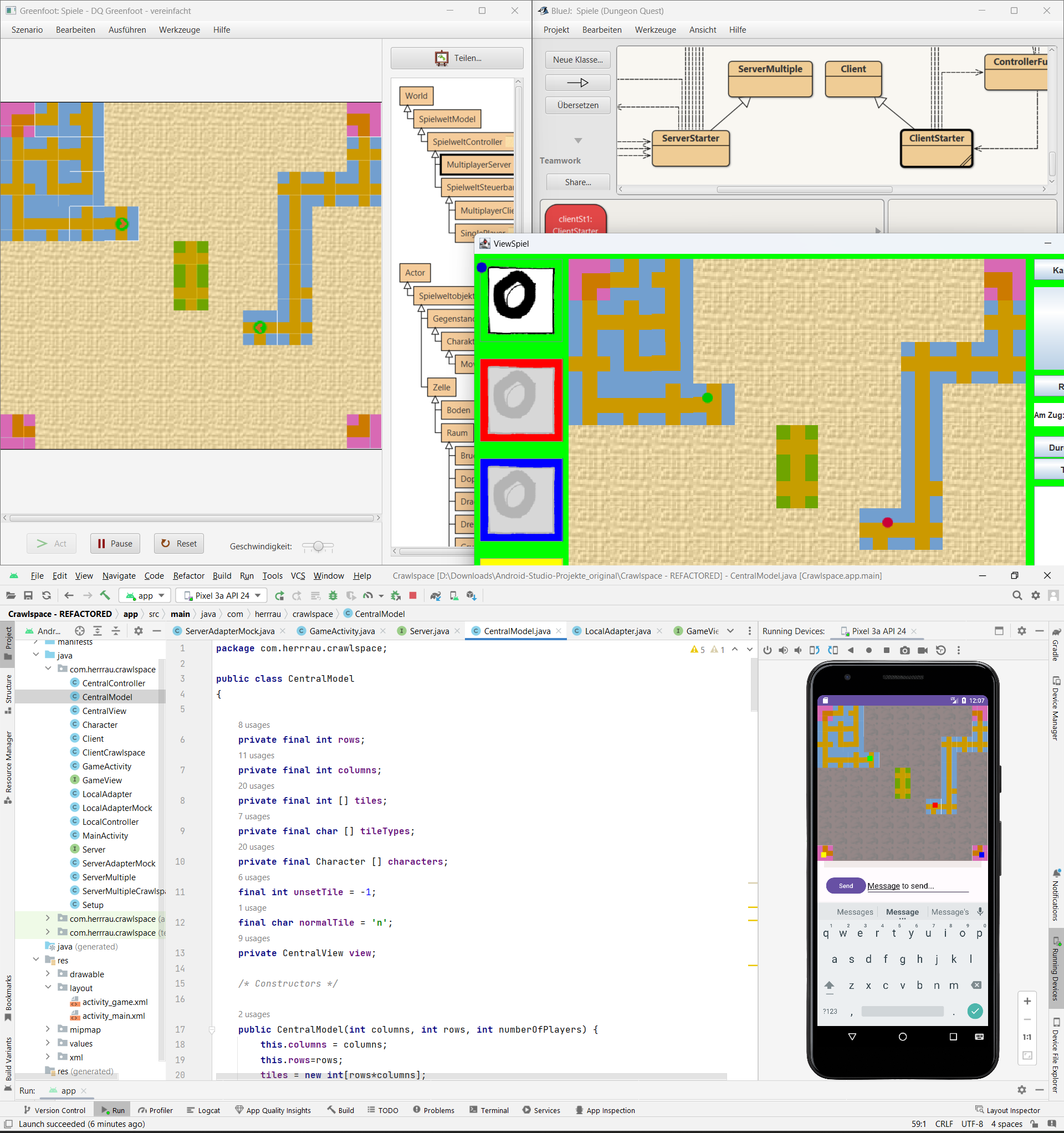
Ein Spiel in Android programmieren
(3 Kommentare.) Schon vor ein paar Jahren hatte ich ein Spiel-Grundgerüst in Java programmiert, erst in BlueJ, dann in Greenfoot, das sind zwei Entwicklungsumgebungen für die Schule. Aus einer Laune heraus wollte ich das jetzt für Android haben. 2018 hatte ich eine Fortbildung in Dillingen dazu gemacht, das wollte ich auch mal umsetzen. Der aktuelle…
-

Meine erste App (öffentlicher Betatest)
(4 Kommentare.) Datenschutzerklärung: Die App sammelt keine Daten. Einziger Kontakt zum Internet besteht bei der expliziten Abfrage des Mensa-Speiseplans, dort wird eine https-Anfrage an den gemieteten Schulserver gestellt. Dabei fallen die üblichen übermittelten Daten an (IP-Adresse), werden aber nicht egspeichert oder verwertet. Schon letztes Jahr habe ich mit dem MIT App Inventor 2 eine App…
-

Eine kleine Programmieraufgabe…
(11 Kommentare.) …die sich als aufwändiger und lehrreicher herausgestellt hat, als ich dachte. Es begann damit, dass ein Kollege mir von dem Computerspiel erzählte, das ihn gerade beschäftigte: Als Schiffbrüchiger auf einer Insel sammelt man unter anderem Gegenstände ein und erntet Pflanzen, jagt Tiere und arbeitet mit Werkzeugen. Zum Beispiel kann man mit einem Messer…
-
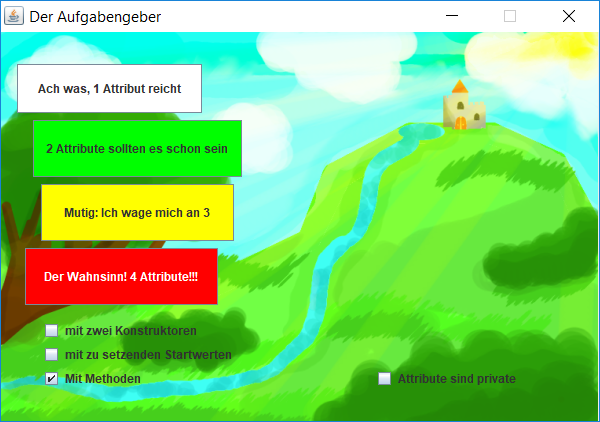
Der Java-Klassendiagramm-Implementierungs-Aufgaben-Generator
(11 Kommentare.) Nachtrag: aktualisierte Fassung des Programms ist am Ende des Beitrags Das mit dem Verstehen ist ja schön und gut, aber bei Sprachen – Programmiersprachen wie anderen – reicht es nicht, wenn man die grammatischen Kategorien kennt, man muss die Sprache auch anwenden können. In Bayern lernen die Schüler in Informatik in der 10.…
-
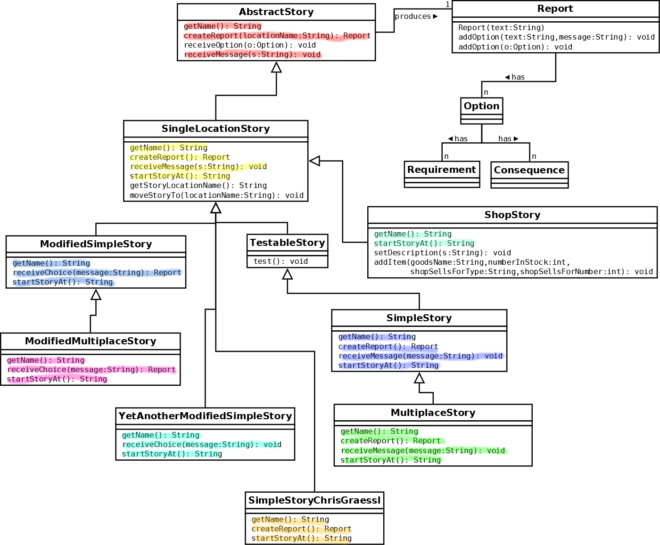
Storyworld – ein Java-Projekt für die 10. Klasse
(11 Kommentare.) Paket für ILTB 2017 Download, Zip, ~20 MB (enthält Präsentation, Anleitung, Code) Storyworld habe ich als Projekt für 10. Klassen am Gymnasium in Bayern im Rahmen des Fachs Informatik durchgeführt. Es geht dabei darum, dass Schülerinnen und Schüler für eine gemeinsame Fantasy-Spielwelt Geschichten schreiben, die in Form von Zustandsautomaten umgesetzt werden und die…
-

Das Geister-Registrierungs-Gerät: Ein Pokémon-Go-Simulator
(4 Kommentare.) Wie hoffentlich die Hälfte aller Informatiklehrer mache ich mir gerade Gedanken, wie ich das allgemeine Interesse an Pokémon Go für die Schule nutzbar mache. (Level 14 übrigens, und wenn ich ein neueres Gerät hätte, auf dem das Programm anständig liefe, wäre ich schon weiter.) Ingo Bartling hat sich schon überlegt, was man daran…
-
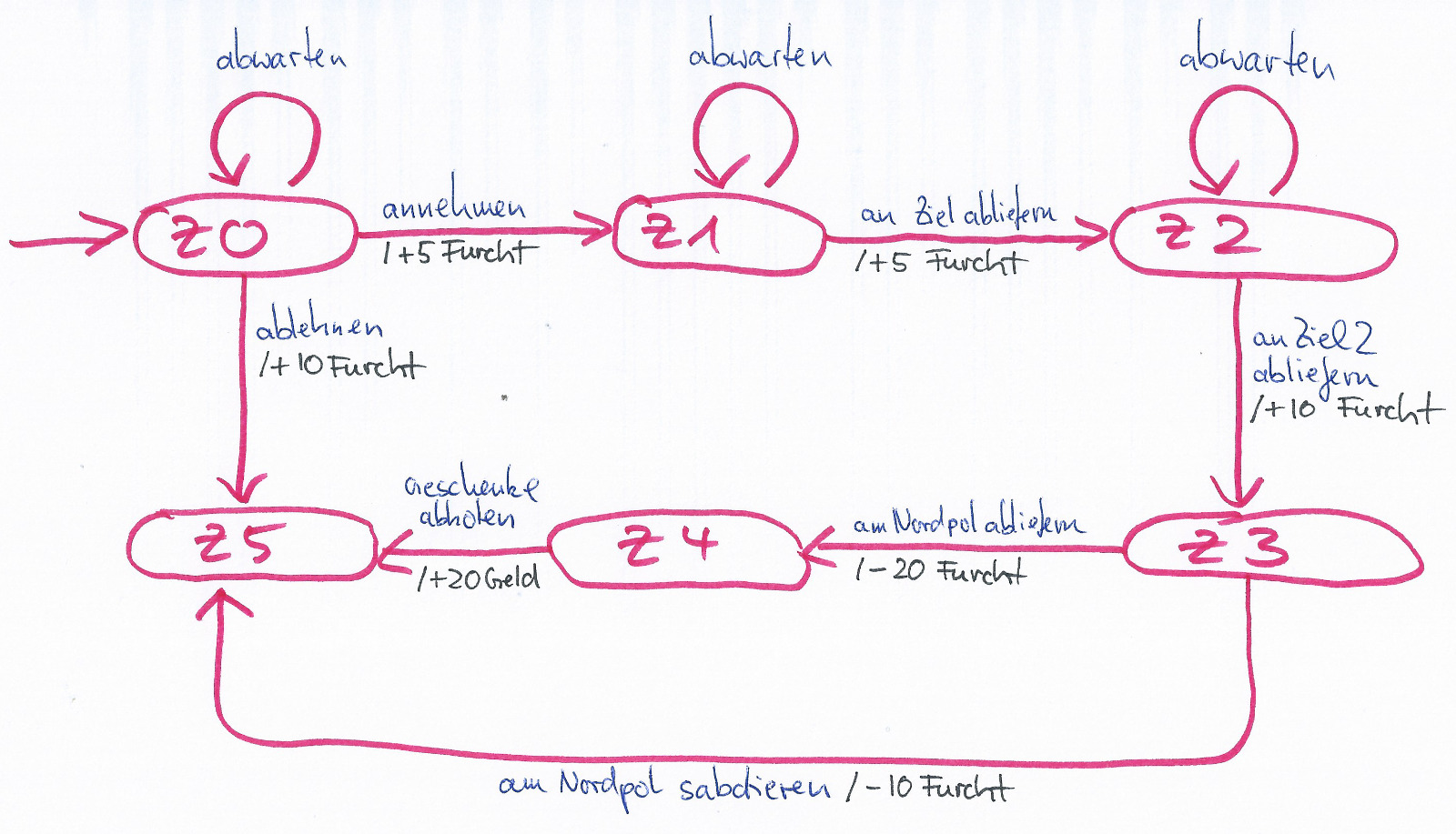
Modulares Geschichtenerzählen in Java, Fortsetzung
(20 Kommentare.) (Fortsetzung von hier, wo ich Sunless Sea beschrieben habe. In der ersten Hälfte geht’s ums Prinzip, in der zweiten wird es dann immer technischer.) Das modulare Prinzip, nach dem in eine bestehende Spielwelt kleine Missionen oder Geschichten eingebaut werden, würde ich gerne für ein Programmierprojekt in der Schule nutzen. Dazu erschafft man gemeinsam…
-
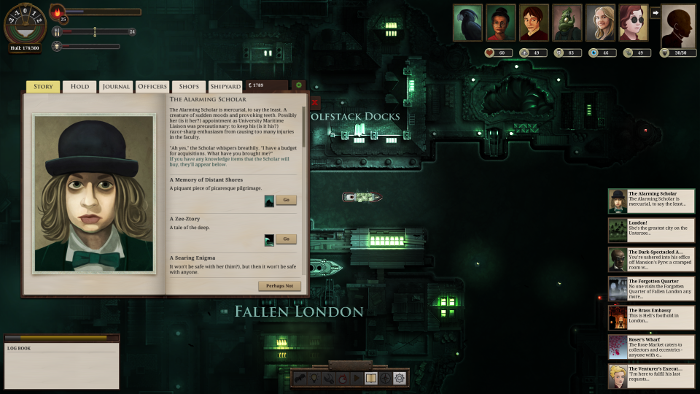
Was ich gerade spiele und warum: Sunless Sea
(4 Kommentare.) Kurzfassung: Ich spiele gerade viel Sunless Sea, und wenn ich überhaupt spiele, was nicht mehr so oft vorkommt, dann meist mit dem Hintergedanken, wie ich das Spiel für die Schule ausschlachten kann. Und bei diesem Spiel hatte ich eine schöne Idee. Vorab: Auf dieses Spiel bin ich gekommen, weil ich zwei sehr empfehlenswerte…
-

Subversion mit BlueJ, die Fortsetzung
(9 Kommentare.) Ich habe vor ein paar Jahren schon mal über Subversion mit BlueJ geschrieben, inzwischen habe ich das mit Schülern weiter erprobt und mit Peter Brichzin einen Workshop dazu auf der INFOS15 gehalten. Subversion: So heißt ein verbreitetetes System, mit dem verschiedene Autoren gleichzeitig an einem aus vielen Dateien bestehenden Progammierprojekt arbeiten können, so…