Fortsetzung von hier. Es geht immer noch nicht um das Erzeugen von Text, sondern um das Ergebnis einer Analyse von Text. Aber darin steckt schon so viel Magie, dass ich das bereits spannend finde. Der Blogeintrag ist bist auf den technischen Hintergrund am Ende hoffentlich leicht zu verstehen, aber er ist sehr lang. Ich habe Frau Rau gefragt, ob ich ihn auf zwei Einträge verteilen soll, aber sie meinte nein, also bleibt er zusammen.

1. Embedding: Einführung des Begriffs

Embedding halte ich für einen ganz zentralen Begriff, um zu verstehen, was bei der automatischen Verarbeitung von Inhalten geschieht.

Nach den N-Grammen waren feste Wort-Embedding-Verfahren die heiße Sache bis etwa 2017. Moderne LLM arbeiten auch mit Embedding, aber noch mit Ergänzungen; mehr dazu ab dem nächsten Mal. Vielleicht.

Embedding heißt allgemein: Ein Wort (oder Token, oder ein ganzer Text, oder ein Bild) wird in eine Zahlenreihe umgewandelt. Zahlenreihe: das heißt fachsprachlich Vektor. Ein Vektor hat eine Länge, aber vor allem hat er eine bestimmte Anzahl an Zahlen, das heißt, er befindet sich in einem Raum einer bestimmten Dimension. Vektoren in einem zwei- oder dreidimensionale Raum aus zwei beziehungsweise drei Zahlen und man kennt sie vielleicht aus der Schulmathematik; wir beschäftigen uns hier eher mit Vektoren in Räumen mit 300 Dimensionen, also 300 Zahlen. Das englische Wort „year“ kann zum Beispiel durch folgenden Vektor repräsentiert werden:

[-0.025786, -0.042872, 0.017601, 0.063622, -0.103329, 0.023634, 0.054678, 0.040233, -0.051739, -0.064657, 0.023516, 0.033084, 0.090718, 0.051757, -0.013683, -0.097553, 0.067920, -0.079240, -0.076960, 0.099556, -0.005586, 0.087658, 0.021216, -0.030638, 0.090439, -0.043562, 0.046424, -0.070301, -0.073923, -0.085469, -0.028303, -0.072659, 0.055611, -0.092044, 0.070280, -0.034189, 0.078083, 0.056718, 0.015751, -0.049231, 0.043795, 0.046121, -0.010422, -0.021453, -0.048846, -0.048375, 0.018076, -0.139829, -0.001987, 0.070634, -0.099343, -0.025047, -0.002585, 0.108708, -0.068641, 0.086222, 0.025860, -0.030051, 0.036753, -0.005112, -0.008837, -0.009897, 0.013929, 0.026580, -0.013089, 0.020542, -0.060059, 0.062302, 0.095074, 0.023722, 0.034571, -0.059392, -0.000980, -0.000784, -0.061180, -0.069526, -0.018580, -0.118761, -0.012066, -0.083601, -0.028266, 0.088769, -0.012761, 0.118279, -0.012628, 0.020282, 0.053124, -0.029784, -0.087240, 0.028490, -0.002649, -0.028264, 0.074022, 0.044470, -0.046292, 0.062624, 0.027311, 0.075023, -0.005248, 0.025290, 0.033313, -0.107309, 0.042446, -0.011116, 0.009652, 0.060412, 0.024261, 0.098144, -0.125430, -0.014803, -0.042813, -0.010587, -0.018827, -0.033675, 0.056361, -0.035354, -0.044778, -0.009897, 0.011386, 0.035792, -0.002038, -0.031330, -0.009778, -0.001057, 0.028198, -0.000704, 0.023876, 0.065053, 0.046788, 0.018013, -0.047985, -0.039999, -0.027081, 0.060187, 0.064933, -0.061414, 0.052294, -0.003506, 0.099521, -0.025471, 0.085860, -0.024881, 0.078323, -0.131082, 0.120399, -0.000521, -0.042779, -0.023151, 0.014987, -0.048307, -0.023339, 0.023993, -0.050328, -0.055788, -0.087864, -0.023055, 0.031015, 0.043504, -0.011933, -0.047324, -0.022298, -0.056046, -0.028270, -0.041753, 0.022536, 0.032980, -0.093301, 0.021712, 0.044414, -0.027758, -0.076788, -0.021686, -0.067725, -0.004186, -0.008080, 0.034993, -0.039559, -0.003645, -0.002335, -0.009184, 0.008698, -0.002859, -0.058528, 0.083969, 0.069957, -0.043843, 0.042897, -0.064762, 0.021673, 0.053250, -0.074874, -0.086903, -0.095449, -0.005371, 0.064299, 0.096931, 0.043711, 0.032208, -0.019445, 0.214736, 0.055460, -0.070967, 0.015095, 0.056014, -0.037825, 0.039392, -0.034608, 0.032038, 0.103250, 0.029820, 0.038454, -0.064354, -0.128182, 0.016288, 0.015339, 0.044159, -0.061186, -0.037290, -0.094278, 0.066222, -0.148060, -0.024454, -0.018784, 0.034114, 0.040694, -0.008600, -0.029586, -0.024523, 0.011347, 0.001708, -0.033704, -0.051059, -0.074759, -0.042689, -0.059257, -0.045433, 0.094440, -0.126478, 0.037676, 0.067256, 0.119020, 0.027962, 0.120834, 0.033210, -0.025278, -0.052161, 0.016049, -0.021046, 0.055670, -0.075887, -0.040669, -0.074454, -0.038057, 0.063454, 0.033169, 0.035221, 0.025169, 0.037108, 0.003785, 0.011474, -0.060609, -0.065979, -0.102240, 0.042050, 0.028562, 0.032571, -0.039410, -0.109837, -0.060135, 0.050419, 0.011264, -0.015715, 0.044828, -0.046791, 0.101858, -0.035604, -0.024885, -0.064720, 0.043942, 0.020953, -0.014011, -0.124052, -0.061068, -0.065812, -0.122686, -0.060203, 0.046817, -0.069997, 0.047701, -0.007218, 0.028453, -0.080661, -0.007487, 0.048209, -0.123690, 0.014074, 0.043732, -0.022902, -0.022820, 0.035935]

(Dieses Embedding enstand auf Grundlage des British National Corpus. Auf diese gesammelten Texte wurde ein Algorithmus angewendet, der jedem Wort im Korpus einen Vektor aus 300 Zahlen zuweist. Andere Verfahren nutzen kürzere oder längere Vektoren, und das gleiche Verfahren kann natürlich zu unterschiedlichen Ergebnissen führen, wenn man es auf Grundlage unterschiedlicher Textsammlungen anwendet.)

2. Warum Embedding, allgemein?

Erst einmal macht ein Embedding aus Nicht-Zahlen Zahlen, und mit Zahlen lässt sich besser rechnen. Aber eigentlich besteht ein Bild, besteht ein Text ja bereits aus Zahlen. Die Zeichenkette „year“ hat zum Beispiel ein Äquivalent aus vier Zahlenwerten, für jeden Buchstaben einen. Warum dann das Umwandeln in 300 andere Zahlen?

Für einen Rechner bedeutet nämlich y-e-a-r nicht viel, egal ob in Buchstaben oder Zahlen, für einen Mensch dagegen: zwölf Monate, und Frühling, Sommer, Herbst und Winter; Jahrestage, 365 Tage und 52 Wochen, und Schaltjahre, und Neujahr und happy new year, und Lichtjahr, und Substantiv und regelmäßiger Plural und another year old and deeper in debt und so viel mehr. Ein Teil dieser Information steckt in den 300 Zahlenwerten des Embeddings.

Ein Bild von 319 x 239 Pixeln Größe mit einer Katze darauf besteht aus 76.241 Zahlenwerten (jeweils mit 2²⁴ Möglichkeiten). Wenn man ein Embedding benutzt, dass viele wesentliche Aspekte des Originals behält und andere weglässt, dafür vielleicht sogar semantische Inhalte ergänzt, hat man eine Reihe von vielleicht 1000 Zahlenwerten (jeweils mit 2^32? Möglichkeiten), mit denen man viel mehr anfangen kann als mit den 76.241 Rohdaten.

Ein Embedding ist also manchmal kürzer, manchmal länger als das Element, aus dem es entsteht, je nachdem, wozu man es braucht. Mit einem kürzeren Embedding lässt sich leichter rechnen und arbeiten und es enthält weniger, aber wesentlichere Information. Ein längeres Embedding hingegen enthält zusätzliche Information.

3. Beispiele für Wort-Embeddings

Auf diese Seite kann man sich verschiedene derart erzeugte Embedding-Sammlungen herunterladen: https://vectors.nlpl.eu/repository/ Es sind große Dateien; hier ein paar Screenshots. Welcher Korpus dabei genau verwendet wurde und welcher Embedding-Algorithmus dazu, steht auf der verlinkten Seite,

Trainiert auf Altgriechisch-Korpus, Vektordimension 100, Ausschnitt:

Trainiert auf der englischen Wikipedia, Embedding-Dimension 300, Ausschnitt:

Was bedeuten die einzelnen Zahlen? Das kann man nicht wirklich sagen. Zusammen bedeuten sie jedenfalls etwas, wenn sie gut gewählt sind.

4. Bedeutung solcher Embeddings

Es stellt sich nämlich heraus, dass in diesen Embeddings ganz schön viel Bedeutung steckt, und das ist kein Zufall, sondern genau die Absicht dahinter.

4.1 Wörter, deren Vektoren näher beieinander liegen, sind sich ähnlicher als entferntere.

Was Nähe hier heißt, sieht man bei zweidimensionalen Vektoren, wie sie einem vielleicht in der Schule begenet sind:

Der Punkt K (1;5) ist näher bei Q (4;3) als bei W (3;-1), das kann man mit dem Geodreieck leicht messen. (Unterschied Punkt, Vektor, Tupel: hier nicht wichtig.) Im dreidimensionalen Raum kann man sich die Entfernung auch noch leicht vorstellen und auch noch mit einem Geodreieck messen. Im 300-dimensionalen Raum geht das eigentlich genauso und ist auch nicht wirklich schwer zu berechnen, nur eben schwer vorzustellen. – Neben der Geodreieck-Entfernung (heißt technisch: euklidischer Abstand) gibt es übrigens auch noch die Manhattan-Entfernung und die Cosinus-Entfernung, wir ignorieren das mal als Feinheiten.

(Cosinus-Entfernung oder -Ähnlichkeit: Das ist das Skalarprodukt der beiden Vektoren, höhere Zahlen bedeuten höhere Ähnlichkeit, bei normierter Vektorlänge zwischen -1 und 1. Glaube ich.)

4.2 Veranschaulichung von Entfernungen

Die folgenden Bilder zeigen die Entfernungen von Embeddings voneinander. Ich habe dazu in Orange einige wenige englische Wörter eingegeben und mir die vorgefertigten fastText-Embeddings dazu geben lassen. Vorgefertigt heißt: die sind auf Grundlage irgendeines seriösen englischen Korpus entstanden, also nicht neu und spontan von mir und Orange berechnet worden. Das ist wichtig, weil es später um anderes gehen wird.

Die Bilder zeigen nicht nur die Entfernung der Embeddings voneinander, sondern versuchen auch sonst etwas Information zu bewahren. Wenn es wirklich nur um die Entfernung gingen, reichte eine Entfernungsmatrix aus. Die 300 Dimensionen der Embeddings kann man natürlich nur sehr, sehr teilweise in die Grafik retten. Auch dafür gibt es einen Algorithmus. Hier die Wörter: auf 2 reduziert, wobei versucht wird, die Entfernung der Vektoren voneinander zu bewahren.

Wir sehen: Die Wörter king/queen, cat/dog, boy/girl, man/woman sind relativ nah beieinander, auch die Gruppe car/bicycle/motorcycle bildet eine Gruppe. Irgendwo in den Vektoren steckt also, dass queen und king mehr miteinander zu tun haben als king und car.

Außerdem sehen wir, dass man ein wenig links unten von woman angeordnet ist, und dass das für die anderen Paare ähnlich gilt. „Unten“ und „links“ sind willkürlich, aber der Algorithmus hat dazu geführt, dass da ein Systen erkennbar wird. Wenn das ein guter Algorithmus war, ist das kein Zufall.

Ich habe die Wörter brother/sister, son/daughter, witch/wizard und royal ergänzt und geschaut, was dabei herauskommt:

Hm. Die Beziehungen zwischen den Paaren ist fast durchgehend erhalten, man/woman sind etwas weiter entfernt, vielleicht um die Beziehungen zu boy/girl mit darstellen zu Witch/wizard ebenso – nur son und daughter sind weit entfernt. Daughter würde ja noch passen, nahe bei sister, was gegenüber von brother – aber son steht eher bei boy/man, car/dog. Ein Artefakt des Abbildungsalgorithmus oder des Embeddings, oder hat das mit der tatsächlichen Verwendung zu tun?

4.3 Die 10 nächsten Nachbarn von…

Auf der Webseite https://projector.tensorflow.org/ kann man eigene Vektorensammlungen hochladen oder aus einigen vorgefertigten auswählen, insbesondere sind Wort-Embeddings dabei. Da kann man sich aus dem (vorhandenen, eingeschränkten) Wortschatz zum Beispiel die 10 nächsten Nachbarn von queen anzeigen, Vektordimension 200:

Die nächsten Nachbarn von queen sind Kollokationen, Antonyme oder Begriffspaare, semantisch verwandte Adjektive, auch Synonyme oder Oberbegriffe. Es sind Wörter, die in einem Texte zusammen mit queen auftauchen oder auch stattdessen.

elizabeth
anne
king
mary
princess
catherine
victoria
royal
scotland
henry
england
marie
duke
crown
empress
vii
monarch
scots
viii
edward
regent
kingdom
lady
kings

Ich habe auf der oben verlinkten Projektor-Seite auch mal einen eigene kleinen Datensatz hochgeladen, dann ist das übersichtlicher, es sind die gleichen Wörter wie oben. Im Screenshot kann man anders als auf der Seite selber das ganze nicht drehen und quasi dreidimensional betrachten:

Auch hier bleiben die Wortpaare beisammen. Die Vektoren dazu habe ich wieder aus dem Embedding anhand des British National Corpus.

4.4 King – Man + Woman = Queen?

Das ist ein berühmtes Beispiel, man begegnet ihm immer wieder. Manche haben sich die Details angeschaut, und es stimmt wohl nicht ganz, oder ist jedenfalls nicht ganz so einfach (Link dazu). Dennoch ist an diese Rechnung etwas dran:

vektor(king) - vektor(man) + vektor(woman) ≈ vektor(queen)

Wenn ich vom Vektor für „king“ den Vektor für „man“ abziehe und den Vektor für „woman“ addiere, lande ich zumindest in der Nähe des Vektors für „queen“. Anders gesagt: „king – man = queen – woman“, oder „king“ verhält sich zu „man“ wie „queen“ zu „woman“.

Hier wieder das Beispiel von oben im 2-dimensionalen Raum:

Ähnliche Wörter haben ähnliche Embeddings, und dann kommt so etwas heraus. Ich glaube, ich habe irgendwann mal die Rechnung mit king, man, queen, woman im 300-dimensionalen Raum gemacht (nicht schwer, die Addition und Subtraktion macht das Tabellenkalkulationsprogramm), aber kein tatsächlich aussagekräftiges Ergebnis erhalten; meine Kenntnisse der Vektorrechnung sind aber begrenzt. Raum für Experimente.

4.5 Vektoren für verschiedene Sprachen

Es gibt auch Modelle, die nach diesem Prinzip mit Texten verschiedener Sprachen trainiert wurden. Dann sind die die Vektoren von Königin und queen benachbart. Das kann beim automatischen Übersetzen helfen oder beim Suchen in mehrsprachigen Dokumentensätzen. Wie viel das wirklich genutzt wird, weiß ich nicht.

5. Embedding von ganzen Texten

Embedding heißt, einem Objekt eine Reihe von Zahlenwerten (einen Vektor) zuzuweisen. Auch ein ganzes Dokument kann man in einen Vektor umformen. Das Ziel ist immer: die relevanten und typischen Merkmale herausarbeiten.

Wenn ich etwa 50 Perry-Rhodan-Hefte vergleichen möchte (Blogeintrag, und Bild unten), etwa um automatisiert erkennen zu können, welches Heft von welchem Autor geschrieben wurde, kann ich die Texte Wort für Wort vergleichen. Aber wie hilft mir das bei der Aufgabe?

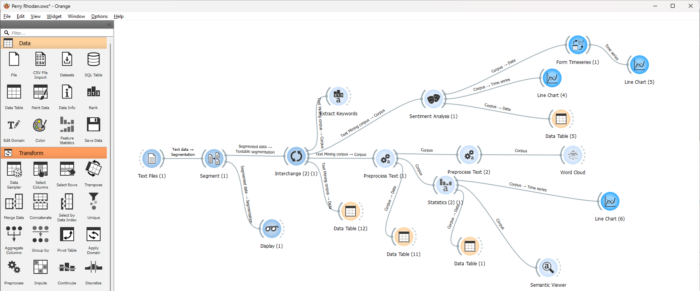
Weil ich meine Pappenheimer kenne, kann ich ein eigenes Embedding erfinden, auch wenn das selbst mittelfristig keine gute Idee ist. Sagen wir, mein Vektor besteht aus: der prozentuale Häufigkeit des Erscheinens der Zeichenkette „Gucky“, vielleicht der durchschnittlichen Wort- oder Satzlänge, der Häufigkeit von Semikolons dazu, der Häufigkeit von „Orgel“ oder „orgelte“? Dann muss ich für die automatische Zuordnung eines neuen Textes zu einem Autor eben nicht den Gesamttext heranziehen, sondern nur die dergestalt aus ihm gewonnenen Werte, das Dokumentembedding. Ein Beispiel- Embedding für zwei Hefte sähe dann so aus:

Author    Atlan Gucky Thora Perry Orgel %Unique WordLength Punctuation
Kurt Mahr     0     0     0     9     0  0.1465      5.304        5049
K.H. Scheer  46    16     0    18     2  0.2054      5.955        4306

Mit diesen Daten kann ich dann arbeiten und vergleichen, und tatsächlich komme ich damit überraschend weit: wenn die durchschnittliche Wortlänge kleiner als 5,42268 ist und mehr als 29 mal „Gucky“ im Text auftaucht, ist das Heft von Clark Darlton. Aber das ist halt genau auf diese 50 Hefte zugeschnitten und würde schon bei den 50 folgenden Heften versagen. Stattdessen gibt es andere, allgemeinere Embeddingverfahren. Orange bietet ein par davon an: Ein einfaches bag of words, ein komplexeres BERT mit 384 Dimensionen oder FastText mit 300 Dimensionen. Dann scheidet in einem Entscheidungsbaum (Informatik 11. Klasse) der Wert von Dimension 20 auf der einen Seite Kurt Mahr und Kurt Brand und auf der andern Seite Clark Darlton, K. H. Scheer und William Voltz. Was die Dimension 20 bedeutet? Das lässt sich, anders als beim selbstgebastelten Embedding, nicht sagen.

6. Embedding von Bildern

6.1 Beispiel: Handschriftliche Ziffern

Ein Bild ist ja bereits eine Reihe von Zahlen: Wenn es 28 x 28 Pixel groß ist, sind das 784 Zahlen. Hier sind 784 solche Zahlen, die jeweils für Helligkeitswerte stehen, in 28 Spalten und Zeilen angeordnet, so dass man bereits ahnen kann, was das Bild darstellt:

Es ist eine Ziffer 7. (Siehe Blogeinträge dazu.)

6.2 Beispiel: Hunde und Katzen

Aber wenn die Bilder komplexer und größer werden, komme ich so nicht weit. Der Vektor zu einem Bild von 4000 x 3000 Pixeln Größe hätte eine Dimension von 12.000.000 statt 784. Ich brauche also ein Embeddingverfahren, das mir diese Dimensionen reduziert, wobei dennoch wesentliche Informationen über das Bild erhalten bleiben, und die auch halbwegs gleich bleiben, wenn ich das Bild rotiere oder verkleinere oder spiegele. Auch hier sollen ähnliche Bilder an ähnlichen Orten im Vektorraun stehen. Und am besten verkürzt das Embedding nicht nur, sondern enthält Information über Farben und Formen und semantische Inhalte – also ob Ampel, Hydrant, Fahrrad auf dem Bild sind.

Für all das gibt es verschiedene Verfahren, und dass das funktioniert, habe ich mit Orange überprüft. Im Web habe ich eine Sammlung von 25.000 Katzen- und Hundefotos gefunden, um damit KI zu trainieren. Die habe ich von Orange einlesen und mit einem Verfahren embedden lassen, die entstandenen Vektoren haben die Dimension 1000, hier sieht man sie im Hintergrund ausschnittsweise als Tabelle:

Im Vordergrund sieht man zwei grafische Darstellungen, und zwar wieder wie bei den Wörtern oben die Abstände zwischen den Vektoren. Man sieht bei den Ergebnissen beider Darstellungsalgorithmen, dass die zwei Vektoren der zwei Gruppen für Katze und Hunde jeweils doch nahe beieinanderliegen, auch wenn man die 999 Dimensionen nicht wirklich abbilden oder sich vorstellen kann. Da ist es nicht verwunderlich, wenn selbst so ein simpler Algorithmus wie kNN (k nächste Nachbarn, Stoff in der 11. Klasse) hohe Prozentwerte beim Zuordnen der Testbilder hat.

Als Gegenbeispiel eine Auswahl der falsch zugeordneten Bilder:

Im folgenden Bild sieht man vier Tierfotos und einen Teil der Embeddings dazu, 1000 Zahlen je Bild. Das Embeddingverfahren wurde – nur um es einmal festzuhalten – nicht mit diesen konkreten Bildern trainiert, es ist ein Standardverfahren (SqueezeNet), das mit vielen anderen Bildern trainiert wurde. Dennoch gelingt es irgendwie, dass diese 1000 Zahlenwerte bei den Katzen und Hunden jeweils untereinander benachbarter liegen als zu der anderen Gruppe.

6.3 Ausblick

Was bei fortgeschrittenen Verfahren auch geht: Dass die Vektoren von Bildern, die Hunde enthalten, dem Vektor dog benachbart sind, und die Katzenbilder dem cat-Vektor. Damit hat man dann eine Brücke geschlagen zwischen der Semantik von Bildern und Wörtern. Wenn man aus vielen Bildern alle mit einer affeetasse herausfinden will, muss man nur nach „Kaffeetasse“ suchen, und dessen Vektor wird mit den Vektorbildern verglichen: https://blog.roboflow.com/what-is-an-image-embedding/

7. Nur kurz zum Algorithmus (wurde dann doch länger)

Für das Embedding von Bildern gibt es verschiedene Verfahren; für das Embedding von Wörtern oder Token natürlich auch: Am bekanntesten ist, heißt es, word2vec, das zum Beispiel in der Bibliothek Gensim implementiert ist; ein ähnliches Verfahren mit anderer Segementierung ist FastText. Das Prinzip bei word2vec ist folgendes: Man nimmt einen Korpus von Texten und lehrt das System vorherzusagen, welches Wort in einer Lücke in einem gegebenen kurzen Kontext steht. Das Ziel ist aber eigentlich nicht wirklich die Vorhersage, sondern das Erzeugen eines geeigneten Embeddings und das Vergleichbarmachen von Wörtern.

(Was jetzt folgt, habe ich mir zusammengelesen; ich bitte, mich auch Fehler aufmerksam zu machen. Ich bin jetzt außerdem nicht so weit gegangen, ein Buch darüber zu lesen, zugegeben. Außerdem weiß ich, dass das alles nicht state of the art ist und nicht unnmittelbar die Weise ist, wie LLMs heute funktionieren; darum geht es mir hier auch noch nicht.)

Zum Berechen der Embeddings benutzt man einfache Neuronale Netze mit nur einer verdeckten Schicht.

• Sagen wir, es gibt ein Vokabular von 160.000 Wörtern in einem Korpus.
• Dann hat das Neuronale Netz 160.000 Eingangsknoten.
• Und die verdeckte Schicht hat, sagen wir, 300 Knoten.
• Und das Netz hat 160.000 Ausgangsknoten.

Wenn man mal nur von einem Wort am Eingang ausgeht (dazu weiter unten mehr), dann bestehen die Eingangsdaten aus einem Vektor der Länge 160.000, der aber fast durchgehend aus 0 besteht, nur an der einen Stelle mit dem Wort ist eine 1, im Bild oben ist das das Vokabular-Element mit der ID 2. Dieses Prinzip heiß „one-hot encoding“, weil nur ein Element aktiv ist.

Dementsprechend sind für dieses Wort auch nur die 300 neuronalen Gewichte interessant, die mit den Kanten dieses einen Eingangsknotens zu den 300 Knoten der versteckten Ebene verbunden sind. Im Bild oben sind das die 3 (stellvertretend für 300) roten Pfeile. Jedenfalls sind diese 300 Gewichte, ta da!, der Embedding-Vektor just jenes Wortes am Netzeingang. Also, wenn das Netz fertig trainiert ist. Ziel des Trainings ist, geeignete Embeddings für Wörter (oder Token) zu erhalten, das Mittel ist die Vorhersage des nächsten Wortes.

Tatsächlich ist es nicht ganz so einfach wie in der Grafik oben. Es gibt zwei Varianten, die beide zu word2vec gehören:

• CBOW (Continuous Bag Of Words), bei dem mehrere Wörter der Input sind, nämlich der Kontext, also die zum Beispiel zwei Wörter vor und nach einer Lücke, und die möglichen Lückenwörter vorherzusagen ist das Ziel, auf das hin trainiert wird.
• Skip Gram, bei dem ein Wort der Input ist, und es gilt vorherzusagen, mit welcher Wahrscheinlichkeit alle anderen Wörter innerhalb eines Abstands von – sagen wir wieder: zwei – Wörtern davor und danach erscheinen.

Ich könnte ein wenig mehr zu den Details berichten, aber wer sich wirklich dafür interessiert, ist mit den Links am Ende des Blogeintrags wahrscheinlich ohnehin besser beraten.

Wenn zwei Wörter – slow und fast oder quick – häufig in ähnlichen Kontexten auftauchen, dann ist auch die Wahrscheinlichkeitsverteilung für die vorhergesagten Kontext-Wörter am Ende des Netzes ähnlich. Und das geschieht vor allem dann, wenn die Gewichtungen in der versteckten Ebene ähnlich sind. Und das heißt, dass die Gewichtungs-Vektoren im Vektorraum nicht zu weit von einander entfernt sind. So entsteht die Nähe im Vektorraum.

8. Fazit

Eine ganze Menge Magie liegt schon in den Embeddings, bevor es überhaupt erst an das Generieren von Texten geht. In diesem Blogeintrag ging es nur um das auf Grundlage eines Korpus einmalig errechnete statische Embedding von Wörtern. Mit denen kann man bereits etwas anfangen, zum Beispiel eine sentiment analysis: Ich könnte eine Menge Tröts bei Mastodon automatisiert dahingehend analysieren, ob sie eine eher positive oder negative Stimmung haben, oder bei einem längeren literarischen Text sehen, wie sich das bei dem verändert. (Meine eigenen Experimente dazu waren aber noch wenig erfolgreich; ich habe se aber nur oberflächlich betrieben.)

LLMs arbeiten mit Embeddings als Ausgangspunkt. Allerdings werden diese Embeddings dann noch einmal geändert, abhängig von ihrer Position im Text. Aber das ist etwas für die nächste Folge, mit der ich dann zunehmend unsicherer werde, und die deshalb möglicherweise etwas auf sich warten lassen wird.

9. Links und Ausprobieren

• vorgefertigte Wort-Embeddings herunterladen: https://vectors.nlpl.eu/repository/ (große Dateien!)
• Abstände vorgefertigter Wort-Embeddings visualisieren: https://projector.tensorflow.org/
• Hier man man drei von vier Wörtern eingeben nach dem Muster von „man“ verhält sich zu „king“ wie „woman“ zu ???, und die Antwort wird berechnet: https://vectors.nlpl.eu/explore/embeddings/en/calculator/#

• Sammlung von je etwa 12.000 Katzen- und Hundebildern: ursprünglich hier https://www.kaggle.com/datasets/karakaggle/kaggle-cat-vs-dog-dataset, dann auch hier: https://github.com/laxmimerit/dog-cat-full-dataset/tree/master

• Tutorial zu word2vec: https://medium.com/@zafaralibagh6/a-simple-word2vec-tutorial-61e64e38a6a1 – sehr ausführlich und dabei in der ersten Hälfte noch verständlich
• Noch ein Tutorial zu word2vec: https://www.geeksforgeeks.org/python-word-embedding-using-word2vec/ (mit Pythoncode zum Ausprobieren, der zumindest bei mir auch läuft)
• Und ein letztes, auch mit Python: https://www.geeksforgeeks.org/word2vec-with-gensim/

Fortsetzung folgt.