Autor: Herr Rau
-

Mein neuer Mantel
(11 Kommentare.) In Wien wies mich Frau Rau beim Flanieren auf einen Mantel in einem Herrenmodengeschäft hin, einen Raglan-Mantel. Der würde mir stehen, meinte Frau Rau; ich pflichtete bei, betrat den Laden, worauf der Inhaber und ich bald handelseinig wurden. Raglan-Ärmel kannte Frau bereits, wusste aber nicht, dass die auf den Raglan-Mantel zurückgehen. Der ist…
-
The Admirable Crichton
(3 Kommentare.) Herr Puntila und sein Knecht Matti In Wien war ich im Theater, habe Brechts Herr Puntila und sein Knecht Matti gesehen. Darin geht es um den reichen Grundbesitzer Puntila, derim betrunkenen Zustand Verbrüderung mit seiner Dienerschaft sucht und sie im nüchternen Zustand klassenbewusst schikaniert. Außerdem will er seine Tochter, wenn er nüchtern ist,…
-
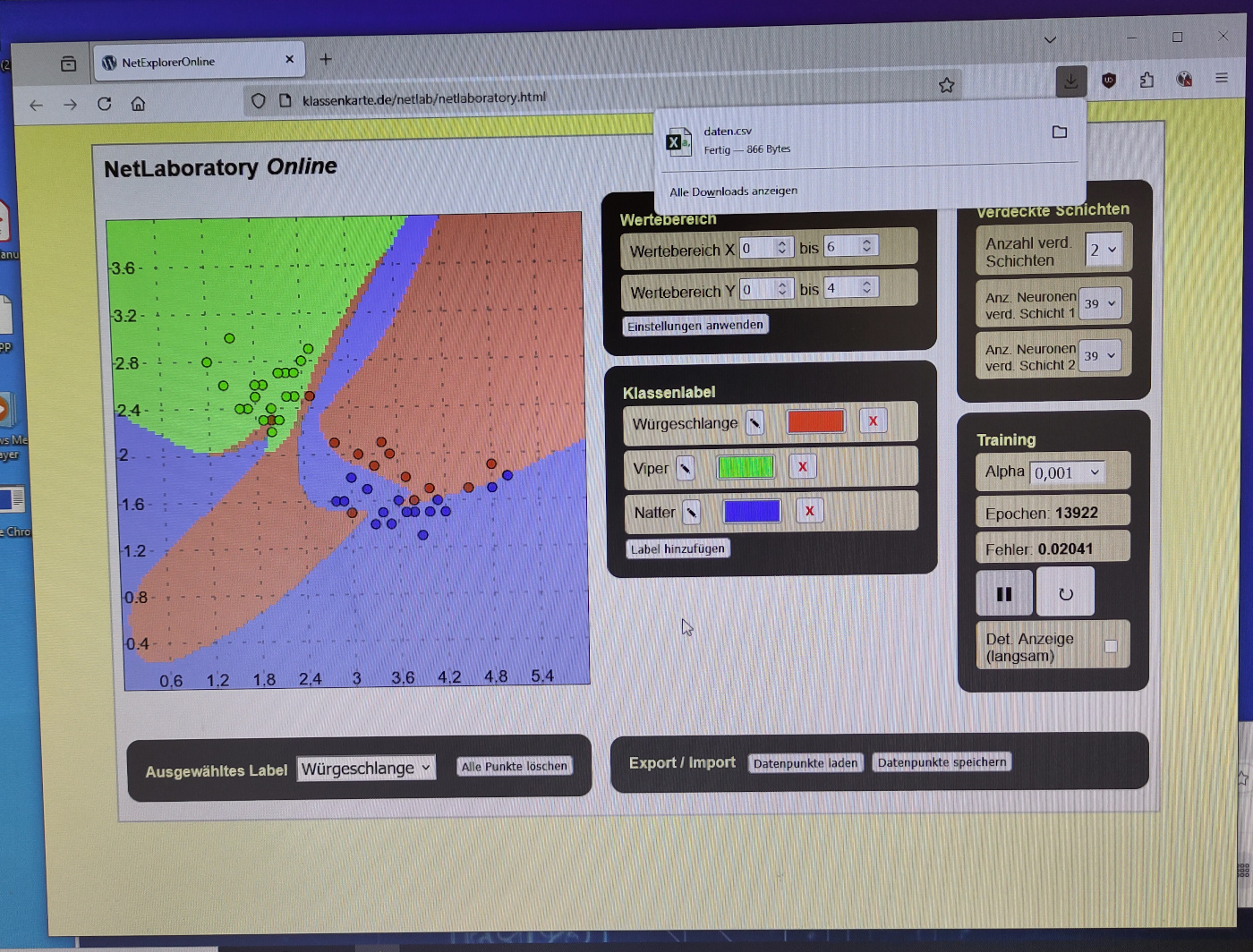
KW 6 und 7, Rückblick
(4 Kommentare.) Zehn Tage ist es her seit meinem letzten Blogeintrag eine meiner längsten Pausen jemals; ich bin erschöpft. Abends koche ich weiterhin leckere Sachen, ich mache soliden Unterricht, aber den Kopf habe ich nicht frei. Eine leichte Erkältung will einfach nicht weggehen, die Eltern werden immer älter und machen Sorgen, wenn auch nicht im…
-
Geht noch mehr Ad-Blocken an Schulen? Und: Linux auf dem Dienstgerät
(4 Kommentare.) Ad-Blocker zuhause Zuhause habe ich in meinem Firefox einen Ad-Blocker als Erweiterung, eigentlich sogar zwei: Adblock Plus und uBlock Origin. Die sind schon so lange darauf, dass ich nicht mehr weiß, warum es zwei sind, und ob ich zwei brauche, und welcher besser ist. Sie wirken sich so aus, dass ich keine Werbung…
-
Sublimierter Ärger über Telefonhotline
(3 Kommentare.) Tröt Der Mensch am Telefon bei der Hotline hat sich so dermaßen viel Mühe gegeben, freundlich zu sein, dass ich mich frage: Kann es sein, dass die Stimmerkennung/KI, der ich zuvor meinen Wunsch mitteilen musste, neben Stimm- auch Stimmungserkennung betreibt und dem Telefonmenschen nicht nur das Stichwort, sondern auch die Stimmung mitteilt (sozusagen…
-
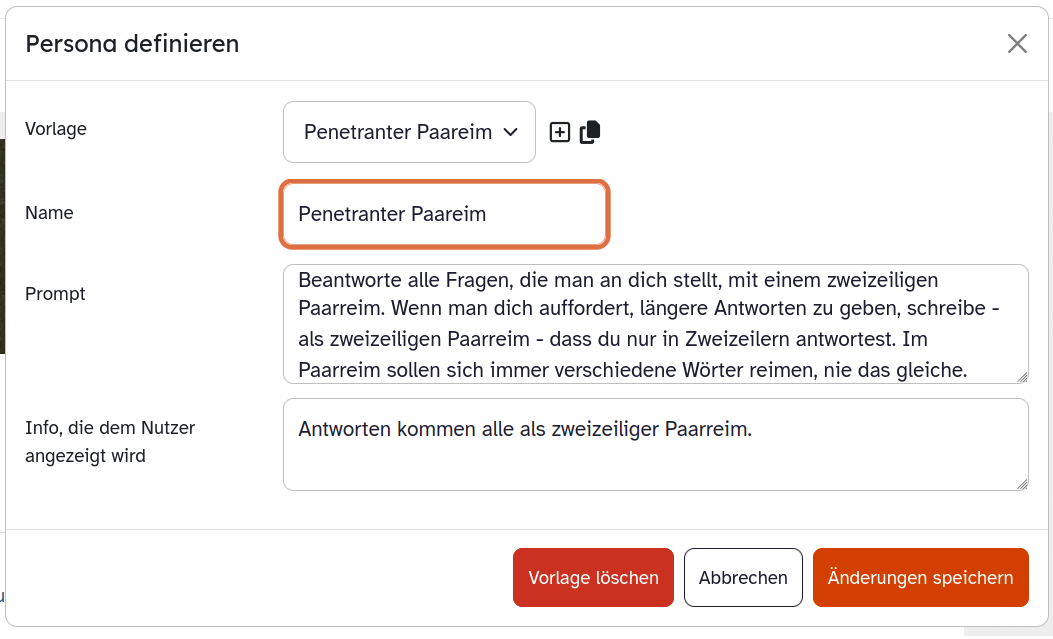
KI in der ByCS
(2 Kommentare.) 1. Anlass Seit Dezember 2025 werden nach und nach für alle interessierten bayerischen Schulen KI-Features in der ByCS-Lernplattform freigegeben, die technisch wohl schon seit einer geraumen Weile existieren und an einzelnen Schulen seit einiger Zeit erprobt wurden. KI heißt natürlich: generative KI. Hier fasse ich diese neuen Elemente zusammen, am Ende geht es…
-

Orangenmarmelade 2026
(7 Kommentare.) Muss ja: Wer Orangenmarmelade will, muss sie machen. Diesmal besonders umsichtig und geplant, so dass die Küche sehr viel weniger klebrig ist als sonst. – Es beginnt immer mit dem Auspressen von einer oder zwei Zitronen, von denen ich nur den Saft und den weißen Glibber innen brauche; die Schale kommt in den…
-
Angelegentliche Beobachtungen, auch zu Versen und Zeilen
(Gesammelte Kleinigkeiten der letzten Zeit.) Stromverbrauch KI Ich betreibe ja dienstlich immer wieder KI, auch wenn ich kein Freund bin. An der Akkulaufzeit merke ich ganz deutlich, wie viel Strom da verbraucht wird. (War auch bei der zweitägigen Fortbildung so, dass allen Laptopnutzenden auffiel, dass am zweiten Tag der Akku viel wenier lang hielt.) Beobachtung…
-
A slug-balancing act?
(3 Kommentare.) Einem Freund zeigte ich vor einem halben Jahr mein Büchlein mit Aufsatzthemen aus dem Jahr 1966, er blätterte darin und hakte – willkürlich ausgewählt – bei einem zu Thomas Manns Novelle „Mario und der Zauberer“ nach. Nun hatte ich die just als Hörbuch angehört, und damit entschied ich, als Oberstufenlektüre noch kurz diese…
-
Die Poesie der Beaufortskala
(4 Kommentare.) Herr Buddenbohm zitiert die Baufortskala, die zur Beschreibung der Windstärke dient, „weil sie so schön klingt, nahezu lyrisch“. Und recht hat er. Auf Wikipedia kann man ihre Geschichte nachlesen und die Formulierungen dazu. Interessant sind speziell die Beschreibungen der beobachtbaren Wirkungen an Land, die zur Einteilung führen: Windstärke 8 große Bäume werden bewegt,Fensterläden…
-

Vom Mausklick zur Maschinensprache (Linux 3)
(7 Kommentare.) 1. Der einfache Teil Es wird wieder technisch. Der erste Teil ist vielleicht noch von allgemeinem Interesse, der zweite Teil dann eher für an Informatik Interessierte, passend zum Stoff in der 13. Jahrgangsstufe in Bayern. (Solange noch Ferien sind, ist Nerdkram erlaubt!) 1.1 Der Klick im Menü Ich habe mir ja im Kontextmenü…
-
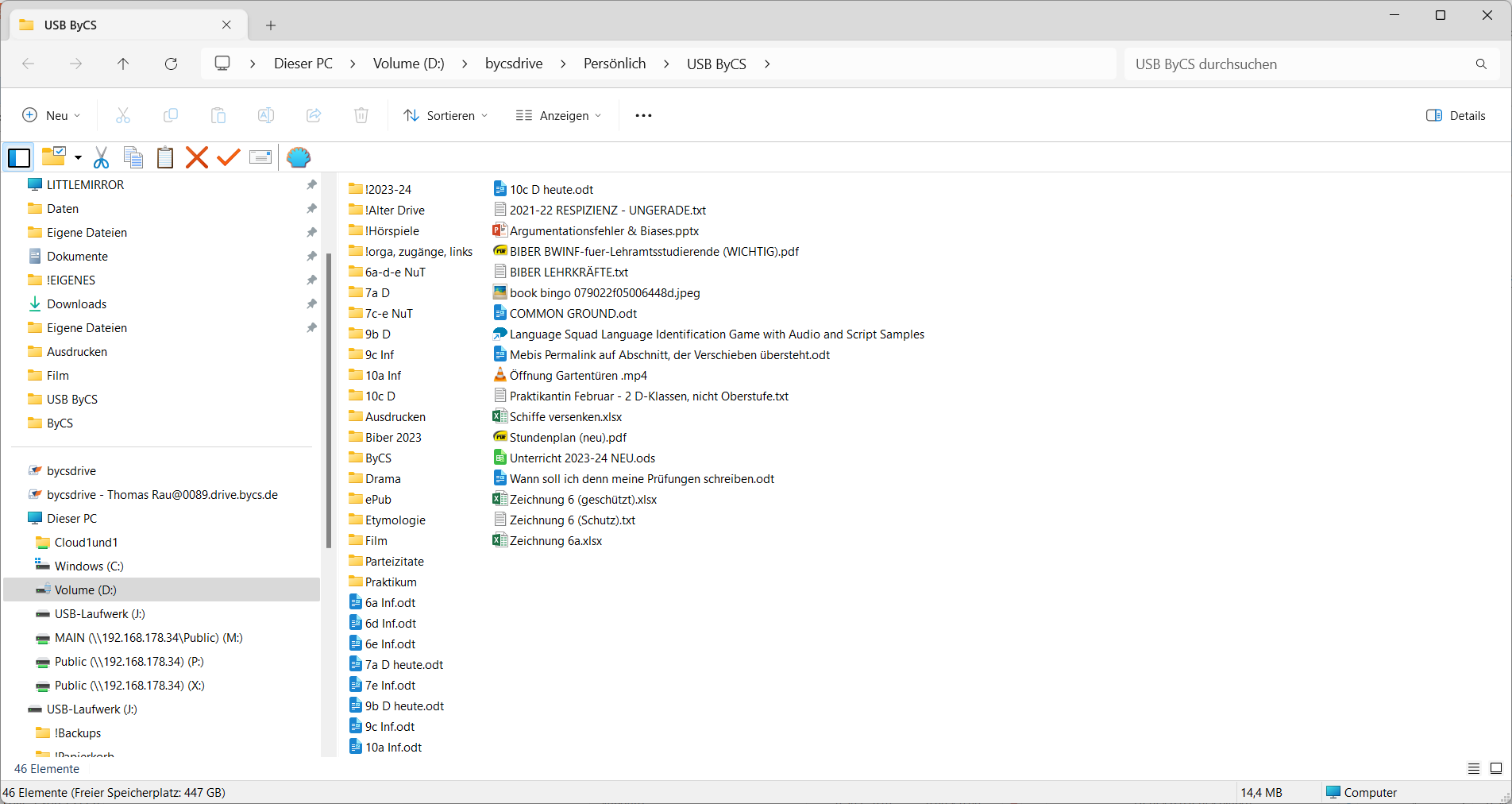
Alles über… ByCS Drive
(2 Kommentare.) 1. Überblick über ByCS-Dienste ByCS heißt BayernCloud Schule und ist der Oberbegriff für eine wachsende Zahl von Diensten, die Lehrkräften und Schüler:innen in Bayern optional zur Verfügung stehen. Einen davon, ByCS Drive, will ich hier kurz vorstellen, vorher aber einen Überblick über andere wichtige ByCS-Anwendungen geben. (Es gibt einen Support für diese Dienste,…