Anfang Juli habe ich in diesem Blog ein kleines Informatikprojekt für das Ende der 10. Klasse vorgestellt: In Java habe ich ein Stein-Schere-Papier-Turnier programmiert. Dabei treten in mehreren Duellen verschiedene STRATEGIEN gegeneinander an. Kernstück ist die Klasse STRATEGIE, die die wichtigsten Methoden enthält, um anhand von Punktestand, Rundenzahl und der vergangenen eigenen Entscheidungen und vor allem denen des Gegners entscheiden zu können, was man jeweils in der nächsten Runde spielt: Stein, Schere oder Papier.
Hier der alte Blogeintrag dazu, der das Konzept ausführlicher vorstellt.
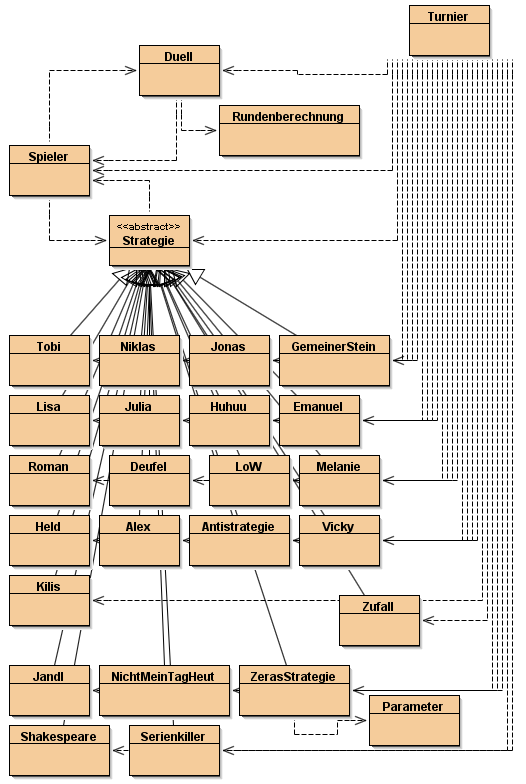
Jeder Schüler musste eine Unterklasse zu STRATEGIE schreiben, und da eine Unterklasse alle Methoden der übergeordneten Klasse erbt, stehen diese den Schüler-Strategien ebenfalls zu Verfügung. Hier das endgültige ursprüngliche, inzwischen in einer neueren Version vorliegende Klassendiagramm:

Hier schreibe ich die Ergebnisse zusammen, allein schon mal deshalb, weil ich das Projekt am 4. Informatiklehrertag in Passau (5. Oktober 2009) in einem Workshop vorstelle.
17 Schüler-Strategien waren funktionstüchtig, 1 war nicht so weit, dass ich sie reparieren konnte, 2 Schüler (mit die erfahrensten am Computer) waren leider nicht da zum Turnier. (Weitere 2 Schüler waren beurlaubt/nicht mehr in der Klasse.) Außerdem nahmen fünf Gaststrategien, die ich hier übers Blog erhalten habe, am Turnier teil.
Das Turnier: Ohne Zufall; einmal jeder gegen jeden; jeweils 100 Runden. 2 Punkte für Sieg, 1 für Gleichstand (also wenn beide das gleiche wählen), 0 für Niederlage. Das heißt, dass bei jedem Duell 200 Punkte in einem Nullsummenspiel zu vergeben sind – wenn der eine Spieler 160 Punkte macht, muss der andere 40 kriegen. Im Schnitt macht jede Strategie 100 Punkte pro Duell, also 1,0 Punkte pro Runde.
Da keine Strategie einen Zufallsgenerator benutzen durfte, sind die Spiele determiniert – es kommt bei jedem Turnier gleicher Länge genau das gleiche Ergebnis heraus. Optional kann man eine Zufallsstrategie mitspielen lassen. Dann schwanken die Ergebnisse ganz leicht, aber wirklich nur leicht. Die Zufallsstrategie hat immer etwa 1,0 Punkte pro Runde – was kein Wunder ist. Egal, gegen wen oder welche Strategie eine reine Zufallsstrategie spielt, sie gewinnt immer etwa ein Drittel der Runden, zieht bei einem weiteren Drittel gleich und verliert etwa ein Drittel, kriegt also 100 von 200 Punkten. Es ist schwer, eine Zufallsstrategie zu schlagen. Es ist aber auch schwer, von ihr geschlagen zu werden.
Deswegen durfte ja keine mitspielen. Von Menschen geschriebene, determinierte Strategien neigen dazu, in Mustern zu spielen oder bestimmte Entscheidungen häufiger als andere zu treffen. Wenn eine andere Strategie diese Muster erkennen kann, ist sie im Vorteil.
Die Gewinner: Hier alle Teilnehmer und ihre durchschnittliche Punktezahl, angeordnet von der Strategie mit den wenigsten Punkten bis zum Sieger:
Vicky hat 0.7361905 Punkte.
Kilis hat 0.7704762 Punkte.
Emanuel hat 0.78095233 Punkte.
Huhuu hat 0.8295238 Punkte.
gemeiner Stein hat 0.91571426 Punkte.
Serienkiller hat 0.9190476 Punkte.
Alex hat 0.92904764 Punkte.
Held hat 0.93 Punkte.
Lisa hat 0.9671428 Punkte
loW hat 0.96952385 Punkte.
Julia hat 0.97761905 Punkte.
Shakespeare hat 0.9809524 Punkte.
Jonas hat 0.98761904 Punkte.
Der Deufel hat 0.99333334 Punkte.
Jandl hat 1.0052382 Punkte.
Melanie hat 1.0290476 Punkte.
Roman hat 1.0738095 Punkte.
Tobi hat 1.0909524 Punkte.
Die Antistrategie hat 1.1057142 Punkte.
Niklas hat 1.1380953 Punkte.
Zeras Strategie hat 1.2952381 Punkte.
Nicht-mein-Tag-heut hat 1.5747619 Punkte.Platz 1, „Nicht-mein-Tag-heut“ und Platz 2, „Zeras Strategie“, sind beides Gaststrategien; die beste Schüler-Strategie, „Niklas“, landet auf dem dritten Platz. Süßwarenpreise wurden an die bestplatzierten Schüler verteilt.
Ein Schnitt von 1,57 heißt, dass „Nicht-mein-Tag-heut“ 57 Prozentpunkte häufiger gewonnen als verloren hat (also zum Beispiel 57% Siege, 43% Gleichstand, 0% Niederlagen; oder 78,5% Siege, 0% Gleichstand, 21,5% Niederlagen).
Variationen:
- Die Langstrecke: Wenn man statt 100 über 1000 Runden spielt, den Strategien also mehr Zeit gibt, die Muster der anderen zu erkennen, verändert sich dann die Rangfolge?
- Zufallsstrategie als Teilnehmer: Dadurch ändert sich nicht viel, außer dass es immer einen Teilnehmer gibt mit einem Schnitt von etwa 1,0 Punkten. Wer besser ist als diese Strategie, der war erfolgreich, wer schlechter ist, nicht.
- Das Überleben der Tüchtigsten: Nach dem ersten Turnier findet ein zweites statt, an dem nur die teilnehmen, die im Turnier zuvor einen besseren Schnitt als 1,0 hatten. Danach macht man ein drittes Turnier, und notfalls weitere, bis man zum Schluss nur noch zwei überlebende Strategien hat.
- Tag team: Mehrere Instanzen der Strategien spielen gegeneinander. So kann eine Instanz der anderen Punkte zuschanzen. Variante: Das geht auch, indem man mehrere verschiedene Strategien ins Turnier zuschickt, von denen einige nur Unterstützer sind und der Hauptstrategie ihre Punkte geben.
- Einzelduelle: Auch die Gewinnerstrategie gewann im Einzelduell nicht gegen alle Mitspieler. Tatsächlich spielte sie gegen eine andere Strategie unentschieden und verlor gegen zwei weitere. Platz 4 , „die Antistrategie“, gewann gegen 12 Mitspieler und verlor gegen 7 (bei 2 Gleichstand), der besser platzierte Platz 3, „Niklas“ dagegen gewann nur gegen 10 Strategien (bei viermal Gleichstand und 7 Niederlagen). Wie ist das zu erklären? „Niklas“ hatte zwar seltener mehr Punkte als sein Gegner, aber wenn er das hatte, dann räumte er wohl mit deutlicherem Abstand ab als „die Antistrategie“. Hier sieht man die Ergebnisse der einzelnen Duelle in einer Matrix. Was fehlt, ist der Abstand zwischen Gewinner und Verlierer, und der ist für die Gesamtpunktzahl und die Rangfolge sehr wichtig.

Rot heißt Niederlage, bzw. Gewinn für Spieler 2. Blau heißt Sieg, bzw. Gewinn für Spieler 1. Gelb ist Gleichstand.
Die Analyse: Warum gewinnen manche Strategien? Was gab es überhaupt für Strategien?
Es gab simple und komplexe Strategien. Bei den Schülern ging das von 16 bis 151 Zeilen Java-Code. Die siegreichen Gaststrategien hatten über 200 Zeilen. Generell haben die komplexen Strategien besser abgeschnitten als die simplen. Bis auf „Niklas“, die beste Schülerstrategie, die gegen den Gewinner „Nicht mein Tag heut“ sogar Gleichstand schafft. Ich habe nicht die geringste Ahnung, warum „Niklas“ so gut abschneidet. Die Strategie wählt in der ersten Runde „Papier“ und in allen nachfolgenden Runde genau das gleiche, was der Gegner in der Runde zuvor gewählt hat. Also: nicht das Gegenteil dessen, sondern das gleiche. Gegen eine simple Nur-Stein-Strategie würde „Niklas“ immer mehr oder weniger einen Durchschnitt von 1,0 erbringen, also Gleichstand. Tatsächlich verliert „Niklas“ gegen 7 Strategien (nur knapp?) und gewinnt gegen 10 (dafür hoch?). „Deufel“, „Antistrategie“, „Melanie“, „Serienkiller“, „Jandl“ und „Roman“ gewinnen öfter als „Niklas“, haben aber jeweils weniger Punkte im Endergebnis.
Die Gewinnerstrategie „Nicht-mein Tag-heut“ gewinnt gegen 18 andere Strategien, spielt unentschieden gegen „Niklas“ und verliert im Duell lediglich gegen „Roman“ und „Melanie“ – allerdings nur auf die Standarddistanz, bei 1000 statt 100 Runden gewinnt in allen Fällen „Nicht-mein-Tag-heut“, wenn auch unterschiedlich knapp (gegen „Niklas“ mit nur 1 Spiel Unterschied, gegen „Melanie“ mit 11, gegen „Roman“ mit 93).
Lässt man nur diese vier gegeneinander spielen, gilt für die erreichte Gesamtpunktzahl allerdings: Niklas > Nicht-mein-Tag-heut > Melanie > Roman, auch auf der 1000er-Langstrecke. Auf der 10.000er-Strecke überholt „Melanie“ bei diesem Vierkampf sogar „Nicht mein Tag-heut“.
(„Melanie“ geht ähnlich vor wie „Niklas“; die Strategie wiederholt die Züge des Gegners jeweils 5 Runden versetzt.)
Einfache und komplexe Strategien: Komplexe Strategien sind die, die so kompliziert sind, dass ich aus dem Programmcode erst einmal nicht schlau werde. Dazu gehören zum Beispiel „Roman“, „Zeras Strategie“ und „Nicht-mein-Tag-heut“. „Roman“ ist mir sehr sympathisch; möglicherweise steckt aber noch ein (semantischer) Programmierfehler drin, so dass die Strategie gar nicht das tut, was sich der Programmierer gedacht hat. Hier die Beschreibung des Schülers:
Meine Strategie berechnet das Rückgabeergebnis anhand der vorherigen Entscheidungen des Gegners. Hierfür benötige ich diverse globale und lokale Variablen und Felder (sowohl zwei- und dreidimensional). Einer Erklärung bedarf es bei den Feldern, die am Anfang deklariert werden:
- zugMod3_counters (zweidimensionales Feld) speichert die Entscheidungen des Gegners (Schere, Stein oder Papier) für runde %3. Dadurch kann ich später unterscheiden, wann der Gegner wie gespielt hat.
- Zum zweiten benötige ich das dreidimensionale Feld zugMod3_wechsel_cnt, indem ebenfalls der Rundenrest und der Wechsel von der vorletzten zur letzten Runde (z. B. von Stein -> Stein, Stein -> Schere, Stein-> Papier ) gespeichert wird.
Nachdem ich diverse Variablen deklariert und initialisiert habe (diese brauche ich meist für den korrekten Speichervorgang in den Listen), schreibe ich vor jeder Entscheidung meinerseits in die Felder, wie sich der Gegner in der letzten Runde entschieden hat. Mit diesen Informationen komme ich ab Runde 3 (vorher wird mehr oder weniger zufällig die Rückgabe über die Nachkommastellen von Pi, die oben in einer Variable gespeichert sind ermittelt) über zwei mögliche Wege zur Rückgabe:
- Entweder es fällt auf, dass der Gegner besonders häufig ein bestimmtes Ereignis auswählt (z. B. Stein). Für diesen Fall nehme ich dann die optimale Gegenoperation (z. B. Papier)
- Oder der Gegner wechselt besonders häufig nach einem bestimmten Zug zu einem bestimmten Ereignis (z. B. häufig von Stein -> Papier). Auch für diesen Fall nehme ich die optimale Gegenoperation (hier: Stein)
Bei beiden Rückgabefindungen beachte ich die aktuelle Lage: vorher in die Listen eingespeicherte Werte verlieren mit der Zeit an Relevanz, da die Werte jede Runde (im oberen Teil) mit 0,98 multipliziert werden. Dadurch vermeide ich, dass mich jemand 40 Runden in die Irre führt und ich dann die letzten 60 Runden ganz einfach ausgetrickst werden kann.
Es gab bisher folgende Arten von Strategien:
- Zufallsartige passive Strategien: für mindestens 100 oder besser noch 1000 oder 10.000 werden die Züge nach einem Zufallsverfahren festgelegt, zum Beispiel über die Dezimalstellen von Pi. Das ist dann immer noch determiniert, aber es lässt sich kein Muster erkennen und jede Entscheidung tritt etwa gleich oft auf (abhängig von der Art des Pseudo-Zufallsgenerators). Solche Strategien dürften im Schnitt immer 1,0 Punkte machen, eben ähnlich wie echter Zufall.
(Die Terminologie aktiv/passiv habe ich vom Programmierer von „Nicht-mein-Tag-heut“ übernommen.) - Einfache passive Strategien: Stein, Schere und Papier werden nach einem mehr oder weniger simplen Muster wiederholt, ohne dass die Züge des Gegenspielers dabei eine Rolle spielen. Solche Strategien können gegen mustererkennende Strategien hoch verlieren. Streng genommen gehört auch der Pseudozufall hierher, nur dass da die Wiederholung erst sehr spät (effektiv: gar nicht) eintritt.
- Einfache aktive Strategien: Das sind solche, die ihre Entscheidung jeweils von einer konkreten Entscheidung des Gegners abhängig machen (der letzten, oder vorletzten oder fünftletzten; vielleicht auch der letzten zwei oder drei). Manchmal erstaunlich erfolgreich („Niklas“, „Melanie“), manchmal nicht („Deufel“).
- Komplexe aktive Strategien: Die versuchen, Muster in den vergangenen Entscheidungen des Gegners zu erkennen. Im einfachsten Fall zählt die Strategie nur mit und reagiert auf die relativen Häufigkeiten der bisherigen Entscheidungen; bei anspruchsvolleren Strategien, wie den beiden Gewinnern, wird gezielt nach bestimmten Arten von Mustern gesucht. Das ist bisher am erfolgreichsten.
Schönheitsfehler: Manche Strategien funktionieren erst bei Duellen mit mindestens 10 oder 12 Runden und sind auf kürzere Duelle nicht eingerichtet; andere melden Fehler bei Duellen, die länger als 200 Runden sind. Das ist kein großes Problem, da für das Turnier von Anfang an Duelle von 100 Runden angesetzt waren. Allerdings ist es auch spannend, wie sich das Verhältnis der Strategien auf längeren Distanzen wandelt. Nächstes Mal daran denken.
Gute Idee: Jeder Schüler musste eine Textdokument abgeben, dass seinen Namen enthielt, seinen Programmcode, und eine Beschreibung dessen, wie die jeweilige Strategie vorgeht. Das war sinnvoll, denn manchmal führten leicht behebbare Programmierfehler dazu, dass sich das Programm anders verhielt als beschrieben. Außerdem sollten die Schüler erklären, warum sie sich für diese Strategie entschieden hatten. So werden die Schüler mit dem Thema Dokumentation vertraut gemacht.
Hilfreich: Diesmal haben die Schüler recht rasch das Modulo-Rechnen kapiert. Viele Strategien benützen etwas wie: „jeder 5. Zug“ – und das geht am einfachsten mit modulo 5, in Java etwa: if (rundeMitteilen()%5==0). Modulo-Rechnen heißt, den Rest bei der Division auszurechnen. 17 modulo 5 (17%5) ist 2, weil ein Rest von 2 bleibt; 39%5 ist 4, 40%5 ist 0.
Durchführbarkeit: Der Stoff der 10. Klasse ist zu viel für die Schüler. An ein Projekt ist dabei eigentlich kaum zu denken. Lehrplan und Buch gehen davon aus, dass fähige Schüler die Klassen TURNIER und DUELL und STRATEGIE ganz oder teilweise selber programmieren. Vielleicht. Sehr vielleicht könnte man das die Schüler selber programmieren lassen. Aber die Zeit dazu hat man nie und nimmer. Ich habe meine Schüler dann doch nur ihre eigenen Strategien schreiben lassen. Manche haben es sich leicht gemacht, andere haben es sich schwer gemacht. Immerhin ist für jeden etwas dabei. Man braucht eigentlich nicht viel Zeit, trotzdem hatte ich nicht genug davon und musste hetzen – und es gab keine Gelegenheit, die Strategien nach dem ersten Turnier zu verbessern. Ich hatte zwar den ganzen Juli dafür veranschlagt, aber wegen Konferenzen und anderer Sperenzen gab es in diesem Monat kaum Informatikunterricht.
Für die Zukunft: Das ganze kann man wiederholen, die neue Schulklasse kann sich dabei durchaus an den Gewinnern des Vorjahres messen. Aber mit noch mehr Zeit. Als Alternative zu Stein-Schere-Papier kann man das Gefangenendilemma wählen, aber auch Finchley Central, allerdings wohl mit Zufallsgenerator. Das Spiel, auch per Post spielbar, geht so: Jeder Spieler nennt gleichzeitig einen der Bahnhöfe der Londoner U-Bahn. Wird ein Bahnhof mehrfach genannt, scheiden alle Spieler aus, die ihn genannt haben. Es gewinnt derjenige, der als Erster – aber eben auch als Einziger – den Bahnhof „Finchley Central“ wählt. Man kann also ein Spiel gewinnen, indem man im ersten Zug „Finchley Central“ wählt – solange man das als Einziger macht. (Als Bonn noch Hauptstadt war, hieß die deutsche Variante „Immenburg“ und wurde mit Bonner Bahnhöfen gespielt.)
Oder gleich das ganz Jahr aufs Spielen ausrichten: Wenn ich noch einmal eine 10. Klasse kriege, mache ich das nämlich anders. Peter Brichzin hat ein Konzept entwickelt, bei dem die Schüler nach und nach ein Pacman-Spiel entwickeln und dabei fast alle Inhalte des Lehrplans lernen. Man braucht dazu nur BlueJ mit einer kleinen Erweiterung. Die Schüler erhalten dazu eine PDF-Datei mit Anleitung und Aufgaben. Sehr schön gefällt mir, dass an bestimmten Stellen immer wieder aufgefordert wird, das bisher Gelernte in einen Hefteintrag zu packen. Nach jedem Kapitel schaut man als Lehrer, ob die Hefteinträge passen. Auch sonst hat man genug zu tun, das ist kein programmierter Unterricht. Schwierige Punkte (Felder vermutlich) wird man zusätzlich erklären müssen. Am Schluss steht ja ein einfaches, aber spielbares Pacman. Das Projekt heißt Krümel und Monster, die Seite dazu ist leider noch im Aufbau. Das PDF- und Java-Material gibt es aber schon, Peter hat es auch schon mehrfach im Unterricht eingesetzt und stellt es bei Fortbildungen vor – so habe ich auch davon erfahren.

Nachtrag: Hier gibt es das Stein-Schere-Papier-Projekt interaktiv. Keine Erklärungen zur Bedienung, Oberfläche ist schlicht gehalten, weil ich mich nicht sehr für Oberflächen interessiere. Die Strategie „Manuell“ erlaubt es, als menschlicher Spieler gegen eine oder mehrere Strategien zu spielen. Dafür würde ich die Rundenzahl erst mal niedrig setzen.

Schreibe einen Kommentar