Mit Python programmiert. Die Fischpopulation macht der Mathelehrer nach Ostern in seinem Fach, und in Informatik können die Schüler das dann programmieren. Ist noch rudimentär, eine Zoomfunktion fehlt noch, aber immerhinque. Alles selbst gemacht, damit ich mich an Python gewöhne und sehe, welche Funktionen ich den Schülern eventuell zur Verfügung stellen muss. Das Programmieren der Fischpopulation ist einfach, die graphische Darstellung ist schwieriger. Aber auch nicht sehr.

Hintergrund:

Man beginnt mit einer Fischpopulation in einem Teich, deren Zahl man in Form eines Prozentwertes angibt. 0% heißt keine Fische, 100% heißt maximal mögliche Fischzahl.

Die Anzahl der Fische in einem Jahr hängt in diesem Modell von der Anzahl der Fische im Vorjahr ab. Die Formel dafür lautet:

Fischzahl_neu = r*Fischzahl_alt(1-Fischzahl_alt)

oder übersichtlicher

x_n+1 = rx_n(1-x_n)

Der Faktor r ist dabei ein veränderlicher Parameter. Interessant ist dabei, dass sich die Fische früher oder später auf eine feste Population einpendeln, egal, mit welcher Fischzahl x₀ man anfängt:
Wenn man r = 1.5 wählt, pendelt sich die Fischpopulation bei 33% ein. Bei r = 1.6: 0.375. Bei r = 1.9: 0.4736. Bei r = 0.4: 0%

Wenn r größer als 3 wird, geschieht etwas anderes: Die Fischpopulation schwankt zwischen zwei Werten hin und her. Bei r = 3.1 pendelt die Population Jahr für Jahr zwischen etwa 76% und etwa 56%.

(Das alles jeweils unabhängig von der Zahl an Fischen, mit der man beginnt.)

Bei r = 3.5 stellt man wieder etwas anderes fest: Die Fischzahl schwankt jetzt periodisch zwischen vier Werten:

0.500884210307
0.874997263602
0.382819683017
0.826940706591
0.500884210307
…

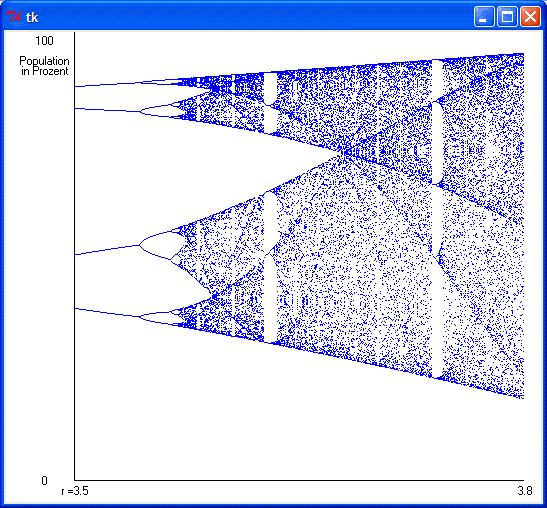
Und so weiter. In der Graphik oben sieht man, was bei immer größer werdendem r als endgültige Fischpopulation herauskommt. An der x-Achse liest man r ab, an der y-Achse liest man die Population ab. Bei niedrigen r ist das 0%: Die Fische sterben aus. Bei größeren r ist das ein fester Prozentsatz, der mit größeren r steigt. Ab r > 3 (ungefähr) schwankt die Fischpopulation periodisch zwischen zwei Werten. Wird r noch größer, schwankt die Population periodisch zwischen vier Werten. Bei r = 3.55 sind es acht Werte, die sich periodisch wiederholen:

0.812655669851
0.54047483399
0.881684346738
0.370325561066
0.827805116599
0.506030509636
0.887370896985
0.354800448
0.812655669851
…

Und wenn r noch ein bisschen größer wird, verdoppeln sich die Perioden weiter und schließlich schwankt die Population wild und nicht mehr periodisch. Mit einer Zoomfunktion könnte man sehen, dass es aber zwischendrin doch immer wieder Inseln der Ordnung gibt – periodische Schwankungen der Perioden 3, 6, 12… oder 7, 14, 28…, bis dann wieder das Chaos beginnt. (Sagt die Literatur.) Der helle Streifen rechts sieht interessant aus. Das muss aber noch warten.

Das ist natürlich alles nicht auf meinen Mist gewachsen, sondern von Robert May, soweit ich weiß.