Monat: März 2010
-
Die Normalverteilung, Teil 1
(16 Kommentare.) Aus Gründen, die ich in einem folgenden Blogeintrag erklären werde, habe ich mich neulich etwas mit der Normalverteilung beschäftigt. Die wird gerne mal von Lehrern und Eltern im Mund geführt. Ich entschuldige mich gleich vorab bei allen Statistik-Erstsemestern, für die das hier alles olle Kamellen sind. Und sicher habe ich auch einige Fehler…
-

Wil Wheaton, Just A Geek
(7 Kommentare.) Just A Geek ist ein autobiographisches Buch. Wil Wheaton erzählt darin von einigen Jahren in seinem Leben, als es ihm nicht so gut ging. Er erzählt in Form von Anekdoten und Erinnerungen, unterhaltsam, aber nicht fröhlich, etwas traurig, aber nicht deprimierend. Aufgehängt ist das ganze an seinen Blogeinträgen aus diesen Jahren, von denen…
-
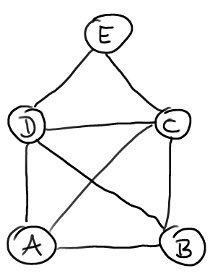
Gemischtes Material zum Graphendurchlauf (Tiefensuche und Dijkstra)
(5 Kommentare.) Ein Graph ist wie die verkettete Liste eine dynamische Datenstruktur. Das ist Stoff im Fach Informatik, 11. Klasse, Bayern. Ein Graph ist im eigentlich nur ein Haufen von Punkten, von denen manche miteinander verbunden sind. Die Punkte heißen auch Knoten und die Verbindungen Kanten. Ein Graph besteht also aus einer Reihe von Knoten…
-
Trochäische Vierheber
(10 Kommentare.) Metrik in der 6. Klasse: 1. Erst mal das Zählen von Silben üben. Was ist eine Silbe, was ist keine? Das Wort „Abend“ hat zwei Silben, auch wenn man in der Silbentrennung nicht „A-bend“ schreiben darf. 2. Das Unterscheiden von betonten und unbetonten Silben üben. Jede Silbe ist im Deutschen eher mehr oder…
-

Stillleben zur Schullektüre
(16 Kommentare.) Ein Quiz: Was lesen wir gerade im Deutsch-LK? Das könnte ich öfter machen; zu jeder Lektüre ein Stillleben mit den wichtigsten Dingen aus dem Buch – Symbolen, Leitmotiven, MacGuffins. Eine Sammlung davon wäre schön, so jeweils als Einstieg zur Besprechung oder Wiederholung. (Und so haben meine Schüle auch mal Udon- und Ramen-Nudeln gesehen.…
-
Was ist eigentlich mit der Feder meiner Tante los?
(17 Kommentare.) Gerade höre ich „Je t’aime“ in der Version des Ukulele Orchestra of Great Britain, voller Klamauk und frrrrranzösischen Wörtern, die nicht unbedingt alle immer zum Lied passen. Zwischendurch kommt auch ein gemurmeltes „la plume de ma tante“. Diese Wörter verfolgen mich mein ganzes Leben begegnen mir immer wieder. Das erste Mal war in…
-
Percy Jackson – Diebe im Olymp
(14 Kommentare.) Am Freitag war ich mit der 6. Klasse im Kino. Den Schülern hat der Film gefallen, das ist das wichtigste. Ich selber fand ihn routiniert, aber profillos. Schön war es allerdings, die griechischen Götter mal wieder zu sehen. Ich bin auch schon auf die Neuverfilmung von „Kampf der Titanen“ dieses Jahr gespannt. Einige…
-
Wochenrückblick, wie angekündigt
(2 Kommentare.) Über den Unterricht habe ich lange nichts mehr geschrieben. Es läuft harmonisch, die Schüler und ich vertragen uns entweder gut oder zumindest viel besser als vor Weihnachten; sie lernen was und mir macht die Schule Spaß. Heute nachmittag gehe ich mit der 6. Klasse ins Kino Percy Jackson – Diebe im Olymp anschauen.…
-
Wieder mal Fundsachen
(5 Kommentare.) Online-Test gibt Aufschluss über eigene IT-Fitness (via TeachersNews): Bei http://www.it-initiative.at. 26 Multiple-Choice-Fragen, die man in 20 Minuten beantworten soll. Die ersten fünf oder sechs Fragen habe ich mir angeschaut, dann genervt aufgehört. Bis auf eine waren alle Fragen rechnerspezifisch (nur PC-Tastatur, nicht Apple), betriebssystemspezifisch (nur Windows, nicht Linux) und programmspezifisch (nur Word, nicht…
-
Vom Schweigen
(9 Kommentare.) Die Schüler der Tendai-Schule pflegten schon die Meditation, bevor Zen nach Japan kam. Vier von ihnen, die sehr gute Freunde waren, versprachen einander, sieben Tage lang Schweigen zu bewahren.Den ersten Tag verbrachten alle schweigend. Sie meditierten einträchtig, aber als der Abend anbrach und die Öllampen nicht mehr genug Licht verbreiteten, rief einer der…