Monat: Januar 2009
-

Life (der Zellautomat)
(2 Kommentare.) Es gibt eine Art Computerspiel namens Life, nach dem Erfinder auch Conway’s Game of Life genannt. Man spielt nicht selber mit, sondern man setzt ein paar Zellen in eine leere Welt und schaut zu, wie sie sich vermehren oder sterben. Das sieht zum Beispiel so aus: Die Regeln für das Überleben, Fortpflanzen und…
-

Cartoons machen mit makebeliefscomix
(4 Kommentare.) Schon vor einiger Zeit beim Webweiser gefunden: makebeliefscomix.com. Dort kann selber Cartoons erstellen, ausdrucken oder einen Link zu ihnen mailen. (Speichern als solches geht nicht, daher Screenshots.) Zum Vergrößern draufklicken. Die Cartoons haben eine Schülerin und ein Schüler aus der 6. Klasse erstellt. Das war so eine Art Kombination aus Informatik und Englisch-Unterricht.…
-
Lernen durch Lehren
(33 Kommentare.) Man liest gerade viel von Lernen durch Lehren. Und das kommt so: An der PH Ludwigsburg gibt es gerade ein Seminar „Didaktik des Informatikunterrichts“. Aus diesem Seminar sind durch Vernetzung verschiedene Projekte entstanden. Schulklassen, Schüler, Lehrer an Schulen und Hochschulen arbeiten zusammen. Jeder könnte mitmachen, und tatsächlich habe ich mich auch angemeldet bei…
-
Werben für den Abistreich? Oder dagegen?
(5 Kommentare.) Ich sage es nicht gerne, aber die Abistreiche der letzten Jahre – eigentlich fast jeder, den ich an dieser Schule erlebt habe – waren lieblos und schlecht organisiert. Die Gastgeber haben sich jeweils mehr oder weniger amüsiert, der Rest nicht. Die meisten Jahrgänge lassen verlauten, dass es bei Ihnen ganz anders sein würde,…
-
Blogtipp: Romantische Schule
(3 Kommentare.) Wer die Romantische Schule noch nicht kennt, sollte sie sich anschauen. Ein Blog-Projekt eines Grundkurses Deutsch (12) mit vielen guten Ideen zur Romantik. Schön vor allem, dass die Schüler unter dem Pseudonym eines Dichters/einer Denkerin der deutschen Romantik bloggen. Im letzten Beitrag werden die von Schülern dazu verfassten Portraits angekündigt. Freue mich schon…
-
Ich trinke das Zeug doch nicht, weil es mir schmeckt
(21 Kommentare.) Wir haben einen neuen Kafeeautomaten im Lehrerzimmer. Der macht Espresso, genau so wie der von George Clooney in der Fernsehwerbung. Und Milchkaffee. Und Cappuccino. Und so. Und alle stehen davor, an die Theke gelehnt, die wir im Lehrerzimmer haben und die tatsächlich zum Lehnen einlädt, und trinken Kaffee aus kleinen Tässchen. Daneben gibt…
-
Bei Lehrers zu Hause
(3 Kommentare.) Hier ein Video aus der Reihe „Puerto Nico erklärt…“ Sehr schön produziert. Den dort – etwa ab 1’50“ – vorgestellten Lehrer kenne ich zwar nicht persönlich, aber er unterrichtet an der Nachbarschule. (Unsere Lehrerskinder gehen gerne dahin und wohl auch umgekehrt.) Da schaut man natürlich besonders interessiert. Gerüchteweise gibt es bei uns seit…
-
Gleich zwei neue Wörter beim Bloglesen gelernt
(3 Kommentare.) Korrekturakne und Korrekturhochzeit. Vor allem für das letztere scheint mir schon lange ein Wort fällig.
-
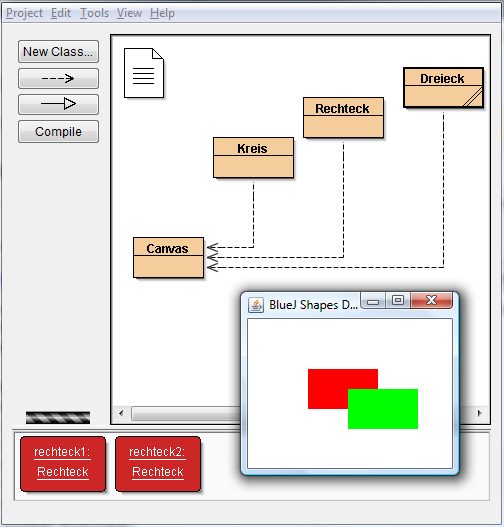
Zwei Arten von Anschaulichkeit
(7 Kommentare.) Unser Informatik-Buch (10) versucht, wie andere auch, Anschaulichkeit in Java dadurch zu erreichen, dass man mit grafischen Klassen wie RECHTECK und KREIS arbeitet. (Programmierumgebung: BlueJ.)In Java sieht das so aus: Das heißt in Java, dass ein Objekt der Klasse Rechteck die Attribute Länge, Breite, Höhe, Füllfarbe haben soll, ebenso auch eine x- und…
-
Patrick McGoohan
Gestorben, mit 80 Jahren, Schauspieler Patrick McGoohan. Ich kenne ihn aus vielen Filmen, aber er wird immer Nummer 6 aus der Fernsehserie The Prisoner bleiben. Hier kann man alle Episoden anschauen. Meine Lieblingsepisode, nichts für Einstieger: „A, B & C“. McGoohan konnte dieses wunderbare Zucken des einen Mundwinkels. Nachtrag: Erinnerungen und Nachruf and ihn. Ebenfalls…
-
Amazon reviews
(6 Kommentare.) Dieses Genre ist mir bisher entgangen: Surreale Amazon-Kritiken. The Secret The Secret – ein Self-Help-Bestseller. Die Kritik beginnt harmlos: „Please allow me to share with you how ‚The Secret‘ changed my life and in a very real and substantive way allowed me to overcome a severe crisis in my personal life.“ Dann wird…
-
Formale Sprachen, Teil 3: Kontextfreie Sprachen
(14 Kommentare.) Das ist die Fortsetzung dieses Eintrags. Aber danach gibt es erst mal wieder Blogeinträge, die vielleicht von allgemeinerem Interesse sind, bevor ich mich dann an die richtig schwierigen Sachen wage. Nehmen wir als Alphabet wieder nur {a, b}. Aus diesen zwei Zeichen kann man unendlich viele Wörter kombinieren. Greifen wir eine Teilmenge davon…